Cho một tấm nhôm hình chữ nhật có kích thước 80cmx50cm. Người ta cắt ở
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
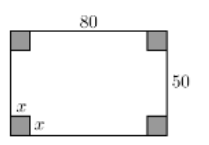
Cho một tấm nhôm hình chữ nhật có kích thước 80cmx50cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $\large x(cm)$. Rồi gập tấm nhôm lại thì được một cái thùng không nắp dạng hình hộp. Thể tích lớn nhất của khối hộp bằng.

Đáp án án đúng là: B
Lời giải chi tiết:
Hình hộp được tạo thành có kích thước chiều dài $\large 80-2x(cm)$; chiều rộng $\large (50-2x(cm)$; chiều cao $\large x(cm)$ (Điều kiện $\large 0
Suy ra thê tích của khối hộp: $\large V=x(80-2x)(50-2x)=4x^{3}-260x^{2}+4000x$
Khảo sát $\large f(x)=4x^{3}-260x^{2}+4000x$ trên (0;25) được $\large\underset{(0;25)}{max}f(x)=f(10)=18000cm^{3}$
Đáp án B
Xem thêm các bài tiếp theo bên dưới
- Cho tứ diện $\large ABCD$ có $\large S_{\bigtriangleup ABC}=4cm^{2},S_
- Cho hình chóp $\large S.ABC$ có đáy là tam giác với $\large AB=AC=5a,B
- Một người xây nhà xưởng hình hộp chữ nhật có diện tích sàn là $\large
- Cho hình chóp tứ giác đều $\large S.ABCD$ có cạnh đáy bằng $\large a$,
- Cho lăng trụ $\large ABC.A'B'C'$ có các mặt bên đều là hình vuông cạnh