Cho lăng trụ $\large ABC.A'B'C'$ có các mặt bên đều là hình vuông cạnh

MỤC LỤC
Câu hỏi:
Cho lăng trụ $\large ABC.A'B'C'$ có các mặt bên đều là hình vuông cạnh $\large a$. Gọi $\large D,E$ lần lượt là trung điểm các cạnh $\large BC,A'C'$. Tính khoảng cách giữa các cặp đường thẳng $\large B'C'$ và $\large A'B$
Đáp án án đúng là: B
Lời giải chi tiết:
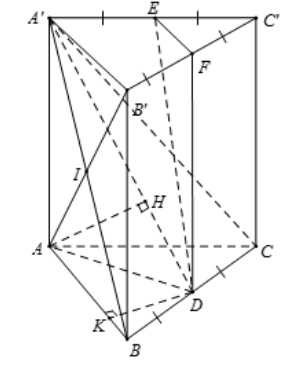
Do lăng trụ $\large ABC.A'B'C'$ có các mặt bên đều là hình vuông cạnh $\large a$ nên $\large ABC.A'B'C'$ là lăng trụ đứng với hai đáy là tam giác đều cạnh $\large a$
Ta có $\large B'C'//BC\Rightarrow B'C'//\left(A'BC\right)$
Suy ra $\large d\left(B'C', A'B\right)=d\left(B'C',\left(A'BC\right)=d\left(B',\left(A'BC\right)\right)\right.$ (1)
Gọi $\large A'B\cap AB'=\{I\}\Rightarrow d\left(B',\left(A'BC\right)\right)=\frac{B'I}{AI} d\left(A,\left(A'BC\right)\right)=d\left(A,\left(A'BC\right)\right)$ (2)
Do $\large ABC$ là tam giác đều cạnh $\large a\Rightarrow AD=\frac{a\sqrt{3}}{2}$ với $\large AD\perp BC(D\in BC)$
Kẻ $\large AH\perp A'D\left(H\in A'D\right) \Rightarrow d\left(A,\left(A'BC\right)\right)=AH$
Xét tam giác $\large A'AD$ có $\large\frac{1}{AH^{2}}=\frac{1}{AA'^{2}}+\frac{1}{AD^{2}}=\frac{1}{a^{2}}+\frac{4}{3a^{2}}=\frac{7}{3a^{2}} \Rightarrow AH=\frac{a \sqrt{21}}{7}$ (3)
Từ (1), (2) và (3) suy ra $\large d\left(B'C', A'B\right)=\frac{a\sqrt{21}}{7}$
Đáp án B
Xem thêm các bài tiếp theo bên dưới
- Cho hình lăng trụ đều $\large ABC.A'B'C'$, đáy có cạnh bằng $\large a$
- Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? A. 2 B. 4 C. 6
- Trong các mệnh đề sau, mệnh đề nào đúng? A. Mỗi hình đa diện có ít nhấ
- Khối đa diện đều loại {4;3} có số đỉnh là: A. 4 B. 6 C. 8 D. 10 Khối đ
- Cho khối chóp là đa giác có 7 cạnh. Trong các mệnh đề sau, đâu là mệnh