Một người xây nhà xưởng hình hộp chữ nhật có diện tích sàn là $\large
MỤC LỤC
Câu hỏi:
Một người xây nhà xưởng hình hộp chữ nhật có diện tích sàn là $\large 1152m^{2}$ và chiều cao cố định. Người đó xây các bức tường xung quanh và bên trong để ngăn nhà xưởng thành ba phòng hình chữ nhật có kích thước như nhau (không kể trần nhà). Vậy cần phải xây dựng các phòng theo kích thước nào để tiết kiệm chi phí nhất (bỏ qua độ dày của bức tường).

Đáp án án đúng là: C
Lời giải chi tiết:
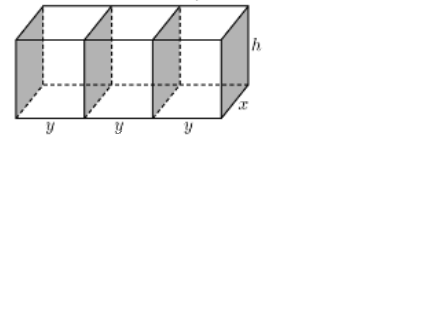
Đặt $\large x,y,h$ lần lượt là chiều dài, chiều rộng và chiều cao mỗi phòng.
Theo giả thiết, ta có $\large x\cdot 3y=1152\rightarrow y=\frac{384}{x}$
Để tiết kiệm chi phí nhất thì diện tích toàn phần phải nhỏ nhất.
Ta có $\large S_{tp}=4xh+6yh+3xy=4xh+6.\frac{384}{x}.h+1152=4h\left ( x+\frac{576}{x} \right )+1152$
Vì $\large h$ không đổi nên $\large S_{tp}$ nhỏ nhất khi $\large f(x)=x+\frac{576}{x}$ $\large (\text {với} x> 0)$ nhỏ nhất
Cách 1.
Khảo sát $\large f(x)=x+\frac{576}{x}$ với $\large x> 0$, ta được $\large f(x)$ nhỏ nhất khi $\large x=24\rightarrow y=16$
Cách 2.
BĐT Cosi $\large x+\frac{576}{x} \geq 2 \sqrt{x \cdot \frac{576}{x}}=48$. Dấu "=" xảy ra $\large\Leftrightarrow x=\frac{576}{x} \rightarrow x=24$
Đáp án C
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp tứ giác đều $\large S.ABCD$ có cạnh đáy bằng $\large a$,
- Cho lăng trụ $\large ABC.A'B'C'$ có các mặt bên đều là hình vuông cạnh
- Cho hình lăng trụ đều $\large ABC.A'B'C'$, đáy có cạnh bằng $\large a$
- Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? A. 2 B. 4 C. 6
- Trong các mệnh đề sau, mệnh đề nào đúng? A. Mỗi hình đa diện có ít nhấ