Trong mặt phẳng $\Large (P)$ cho tam giác $\Large OAB$ cân tại $\Large

Trong mặt phẳng $\Large (P)$ cho tam giác $\Large OAB$ cân tại $\Large O,$ $\Large OA=OB=2a,$ $\Large \widehat{AOB}=120^{\circ}.$ Trên đường thẳng vuông góc với mặt phẳng $\Large (P)$ tại $\Large O$ lấy hai điểm $C, D$ nằm về hai phía của mặt phẳng $\Large (P)$ sao cho tam giác $\Large ABC$ vuông tại $\Large C$ và tam giác $\Large ABD$ đều. Tính bán kính mặt cầu ngoại tiếp tứ diện $\Large ABCD.$

• A.

  A. $\Large R=\dfrac{3a\sqrt{2}}{2}.$

• B.

  B. $\Large R=\dfrac{a\sqrt{2}}{3}.$

• C.

  C. $\Large R=\dfrac{5a\sqrt{2}}{2}.$

• D.

  D. $\Large R=\dfrac{5a\sqrt{2}}{3}.$

Chọn A

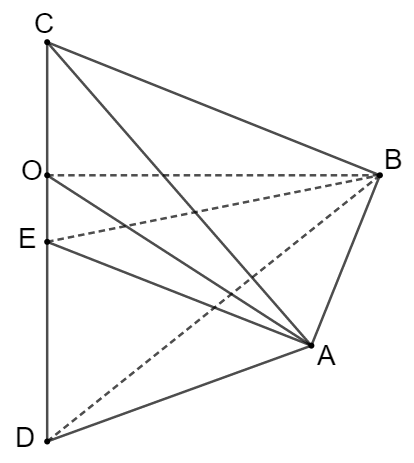
Ta có: $\Large AB^2=OA^2+OB^2-2OA.OB.\cos{120^{\circ}}=12a^2$ $\Large \Rightarrow AB=2a\sqrt{3}.$

Vì tam giác $\Large ABD$ đều $\Large \Rightarrow AD=BD=AB=2a\sqrt{3}$

$\Large \Rightarrow OD=\sqrt{BD^2-OB^2}=2a\sqrt{2}.$

Vì tam giác $\Large ABC$ vuông cân tại $\Large C$ $\Large \Rightarrow 2BC^2=AB^2=12a^2$ $\Large \Rightarrow BC^2=6a^2$

$\Large \Rightarrow OC=\sqrt{BC^2-OB^2}=a\sqrt{2}$

$\Large \Rightarrow CD=OC+OD=3a\sqrt{2}.$

Gọi $\Large E$ là trung điểm của $\Large CD$ $\Large ED=EC=\dfrac{CD}{2}=\dfrac{3a\sqrt{2}}{2}.$

Xét $\Large \Delta ACD$ có $\Large AC^2+AD^2=18a^2=CD^2$

$\Large \Rightarrow \Delta ACD$ vuông tại $\Large A$

$\Large \Rightarrow ED=EC=EA$

Xét $\Large \Delta BCD$ có $\Large BC^2+BD^2=18a^2=CD^2$

$\Large \Rightarrow \Delta BCD$ vuông tại $\Large B.$

$\Large \Rightarrow ED=EC=EB$

Do đó $\Large EA=EB=EC=ED$

$\Large \Rightarrow$ Bán kính mặt cầu ngoại tiếp tứ diện $\Large ABCD$ là $\Large ED=\dfrac{3a\sqrt{2}}{2}.$