Trong không gian Oxyz cho mặt cầu $\Large (S):(x-1)^{2}+(y+2)

MỤC LỤC
Câu hỏi:
Trong không gian Oxyz cho mặt cầu (S):(x−1)2+(y+2)2+(z−3)2=27. Gọi (α) là mặt phẳng đi qua 2 điểm A(0;0;−4);B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), là hình tròn (C) có thể tích lớn nhất. Biết mặt phẳng (α) có phương trình dạng ax+by−z+c=0, khi đó a−b+c bằng:
Đáp án án đúng là: B
Lời giải chi tiết:
+ Vì (α) qua A ta có: −(−4)+c=0→c=−4
+ Vì (α) qua B ta có 2a+c=0⇒a=2
⇒(α):2x+by−z−4=0
+ Mặt cầu (S) có tâm I(1;−2;3),R=3√3
+ Chiều cao khối nón: h=d(I,α)=|2−2b−3−4|√4+b2+1=|2b+5|√b2+5
+ Bán kính đường tròn (C):r=√R2−h2=√27−(|2b+5|√b2+5)2=√27−(2b+5)2b2+5
Thể tích khối nón V=13πr2h=13π(27−(2b+5)2b2+5)|2b+5|√b2+5
+ Tới đây ta làm tự luận như sau:
Đặt t=|2b+5|√b2+5 và xét hàm số f(t)=(27−t2)t trên đoạn [0;3√3]
Ta có: f′(t)=27−3t2;f′(t)=0 ⇔[t=3t=−3(l) Ta có bảng biến thiên
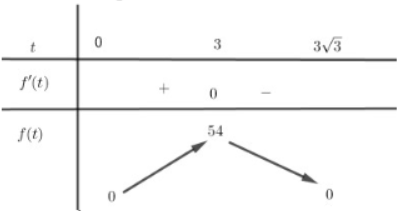
Do đó thể tích khối nón lớn nhất khi và chỉ khi
t=3⇔(|2b+5|√b2+5)2=32⇔4b2+20b+25=9b2+45
⇔5b2−20b2+20=0⇔b=2
Vì vậy a−b+c=−4
Hoặc ta gọi chiều cao khối nón là h, từ phương trình tính thể tích ta suy ra h = 3, tìm b từ phương trình |2b+5|√b2+5=3
Xem thêm các bài tiếp theo bên dưới
- Trong không gian với hệ tọa độ Oxyz, cho $\Large A(a;0;0), B(
- Trong không gian với hệ tọa độ Oxyz, cho ba điểm $\Large A(1;
- Trong không gian với hệ tọa độ Oxyz, cho ba điểm $\Large A(4;
- Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm $\Larg
- Trong không gian với hệ tọa độ cho điểm M(1;0;0) và $\Large N