Trên mặt chất lỏng có hai nguồn sóng kết hợp A,B cùng pha AB = 10cm, đ

Trên mặt chất lỏng có hai nguồn sóng kết hợp A,B cùng pha AB = 10cm, điểm C cách A và B các đoạn CA = 6cm; CB = 8cm, bước sóng là 3cm. Đường cao CH vuông góc với AB tại H. Trên đoạn CH có số điểm dao động cùng pha với hai nguồn là

 

• A. A. 3
• B. B. 2
• C. C. 1
• D. D. 0

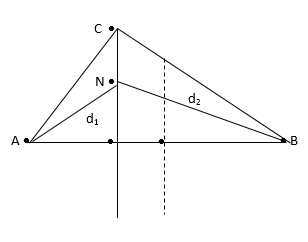
Ta có  CH = 4,8cm; AH = 3,6 cm; BH = 6,4 cm

Xét điểm N trên HC. $\large

Đặt $\large d_1 = AN; d_2 = BN$ với $\large 3,6 \leq d_1 \leq 6 (cm)$

  Giả sử phương trình sóng tại hai ngồn có dạng:

  $\large u = a\cos\pi t (cm)$.

Sóng truyền từ A, B đến N:

$\large u_{AN} = a\cos\left(\omega t - \dfrac{2\pi d_1}{\lambda}\right) ; u_BN = a\cos\left(\omega t - \dfrac{2\pi d_2}{\lambda}\right)$

$\large u_N = 2\cos\dfrac{2\pi(d_2-d_1}{\lambda}\cos\left(\omega t - \dfrac{2\pi(d_1+d_2)}{\lambda}\right)$

  Điểm N dao động cùng pha với nguồn khi: $\large \dfrac{2\pi(d_1+d_2)}{\lambda} = 2k\pi \rightarrow d_1 + d_2 = k\lambda = 3k (*)$

HN = x

$\large d_2^{2} = x^{2} + 6,4^{2}; d_1^{2} = x^{2} + 3,6^{2} \rightarrow d_2^{2} – d_1^{2} = 28 \rightarrow d_2 – d_1 = \dfrac{28}{3k} (**)$

Từ (*) và (**) $\large d_1 = 1,5k - \dfrac{14}{3k} \rightarrow 3,6 \leq d_1 = 1,5k - \dfrac{14}{3k} \leq 6 \rightarrow k = 4$. Có 1 giá trị của k.

  Do đó trên đoạn CH có số điểm dao động cùng pha với hai nguồn là 1