Tọa độ điểm cực đại của đồ thị hàm số $\Large y = x^{4} - 2x^{2} + 1$

Tọa độ điểm cực đại của đồ thị hàm số $\Large y = x^{4} - 2x^{2} + 1$ là

• A.

  A. $\Large (-1; 0).$

• B.

  B. $\Large (1; 0).$

• C.

  C. $\Large (-1; 0)$ và $\Large (1; 0).$

• D.

  D. $\Large (0; 1).$

Chọn D

Tập xác định: $\Large D = \mathbb{R}.$

Ta có: $\Large y{}' = 4x^{3} - 4x$

Cho $\Large y{}' = 0$ $\Large \Leftrightarrow 4x^{3} - 4x = 0$ $\Large \Leftrightarrow \left[\begin{array}{l}x=0 \\x=\pm 1 \\\end{array}\right.$

Bảng biến thiên

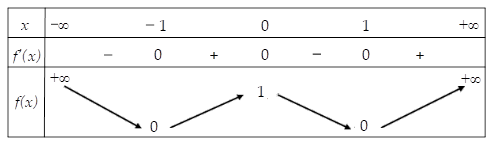
Dựa vào bảng biến thiên ta thấy tọa độ điểm cực đại là $\Large (0; 1).$