Tìm tất cả các giá trị của tham số m để hàm số $\Large y=\mathrm{log}_

Tìm tất cả các giá trị của tham số m để hàm số $\Large y=\mathrm{log}_{2020}(mx-m+2)$ xác định trên $\Large [1; +\infty).$

• A.

  $\Large m \leq 0.$

• B.

  $\Large m \geq 0.$

• C.

  $\Large m \geq -1.$

• D.

  $\Large m \leq -1.$

Chọn B

Cách 1:

Điều kiện: $\Large mx-m+2 > 0 \Leftrightarrow mx > m-2 \ (1)$

Trường hợp 1: $\Large m = 0 \Rightarrow (1)$ trở thành $\Large 0 > -2$ (luôn thỏa mãn).

Trường hợp 2: $\Large m > 0 \Rightarrow (1) \Leftrightarrow x > \dfrac{m-2}{m} \Rightarrow$ Tập xác định của hàm số là $\Large D=\left(\dfrac{m-2}{m}; +\infty\right).$

Khi đó, yêu cầu bài toán trở thành $\Large \dfrac{m-2}{m} < 1 \Leftrightarrow m-2 < m \Leftrightarrow -2 < 0$ (luôn thỏa mãn).

Trường hợp 3: $\Large m < 0 \Rightarrow (1) \Leftrightarrow x < \dfrac{m-2}{m} \Rightarrow$ Tập xác định của hàm số là $\Large D=\left(-\infty; \dfrac{m-2}{m}\right).$ Do đó không tồn tại m thỏa yêu cầu bài toán.

Vậy tất cả các giá trị cần tìm là $\Large m \geq 0.$

Cách 2:

Điều kiện: $\Large mx-m+2 > 0, \forall x \in [1; +\infty) \Leftrightarrow m(x-1) > -2, \forall x \in [1; +\infty) \ (1).$

Với $\Large x=1,$ ta được $\Large 0m > -2,$ đúng với mọi m.

Với $\Large x > 1,$ ta được $\Large (1) \Leftrightarrow m > \dfrac{-2}{x-1}, \forall x \in (1; +\infty) \ (2).$

Xét hàm số $\Large g(x)=\dfrac{-2}{x-1}$ với $\Large x > 1,$ ta có: $\Large {g}'(x)=\dfrac{2}{(x-1)^2} > 0, \forall x > 1.$

Bảng biến thiên:

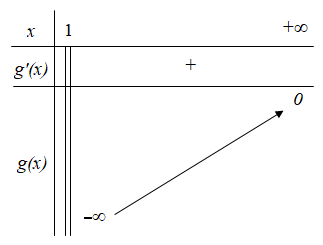
Từ bảng biến thiên, ta được $\Large (2) \Leftrightarrow m \geq 0.$

Vậy, tất cả các giá trị cần tìm của m là $\Large m \geq 0.$