Ông An có một mảnh vườn hình elip có độ dài trục lớn $\Large 12m$ và đ
MỤC LỤC
Câu hỏi:
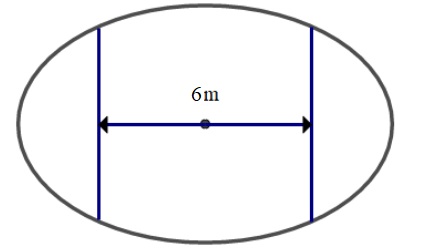
Ông An có một mảnh vườn hình elip có độ dài trục lớn $\Large 12m$ và độ dài trục bé $\Large 8m$. Ông muốn trồng hoa trên một mảnh đất rộng $\Large 6m$ và nhận trục bé của elip làm trục đối xứng như hình vẽ. Biết kinh phí trồng hoa là $\Large 90.000 \,đồng / m^2$. Hỏi ông An cần bao nhiêu tiền để trồng hoa trên mảnh đất đó (số tiền được làm tròn đến hàng nghìn)

Đáp án án đúng là: B
Lời giải chi tiết:
Hướng dẫn:
Ta có độ dài trục lớn $\Large 2a=12\Rightarrow a=6$ và độ dài trục nhỏ $\Large 2b=8\Rightarrow b=4.$
Suy ra phương trình Elip: $\Large \dfrac{x^2}{36}+\dfrac{y^2}{16}=1$ $\Large \Rightarrow \left[\begin{array}{l} y=-\dfrac{4}{6}\sqrt{36-x^2} \left(E_1\right) \\ y=\dfrac{4}{6}\sqrt{36-x^2} \left(E_2\right) \end{array} \right.$
Khi đó diện tích dải vườn được giới hạn bởi các đường $\Large \left(E_1\right);$ $\Large \left(E_2\right);$ $\Large x=-3;$ $\Large x=3$
$\Large \Rightarrow S=2.\int_{-3}^{3}{\dfrac{4}{6}\sqrt{36-x^2}dx}$ $\Large =\dfrac{8}{3}.\int_{0}^{3}{\sqrt{36-x^2}dx}.$
Suy ra số tiền ông An cần là: $\Large T=S.90000$ $\Large =240000.\int_{0}^{3}{\sqrt{36-x^2}dx}$ $\Large \xrightarrow{Casio} \approx 4133000$ (đồng).
Đáp án B.
Xem thêm các bài tiếp theo bên dưới
- Một chất điểm A xuất phát từ vị trí O , chuyển động thẳng nhanh dần đề
- Tính tích phân $\Large \int\limits_{0}^{\dfrac{\pi}{4}}{\dfrac{\ln (\s
- Một cái chuông có dạng như hình vẽ . Giả sử khi cắt chuông bởi mặt phẳ
- Tích phân $\Large I=\int\limits_{-1}^{\dfrac{1}{2}}{\dfrac{4x-3}{\sqrt
- Từ một khúc gỗ hình trụ có đường kính $\Large 30cm$ , người ta cắt khú