Một cái chuông có dạng như hình vẽ . Giả sử khi cắt chuông bởi mặt phẳ
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Một cái chuông có dạng như hình vẽ . Giả sử khi cắt chuông bởi mặt phẳng qua trục của chuông , được thiết diện có đường viền là một phần parabol ( hình vẽ ) . Biết chuông cao 4m, và bán kính của miệng chuông là $\Large 2\sqrt{2}$ . Tính thể tích chuông ?

Đáp án án đúng là: D
Lời giải chi tiết:
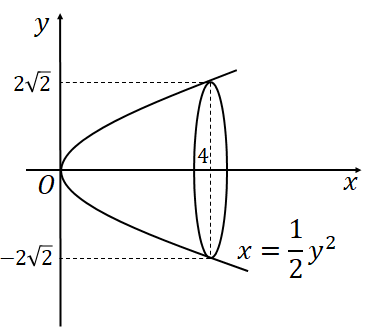
Xét hệ trục như hình vẽ, dễ thấy parabol đi qua ba điểm $\Large(0;0),(4; 2\sqrt{2});(4,-2\sqrt{2}) $nên có phương trình $\Large x=\dfrac{{{y}^{2}}}{2}$ . Thể tích của chuông là thể tích của khối tròn xoay tạo bởi hình phẳng $\Large y=\sqrt{2},x=0,x=4$ quay quanh trục $\Large Ox$ . Do đó
Ta có $\Large V=\pi \int\limits_{0}^{4}{2xdx=\left( \pi {{x}^{2}} \right)\left| \begin{align} & 4 \\ & 0 \\ \end{align} \right.=16\pi }$
Xem thêm các bài tiếp theo bên dưới
- Tích phân $\Large I=\int\limits_{-1}^{\dfrac{1}{2}}{\dfrac{4x-3}{\sqrt
- Từ một khúc gỗ hình trụ có đường kính $\Large 30cm$ , người ta cắt khú
- Một vật đang chuyển động đều với vận tốc $\Large {{v}_{0}}(m/s)$ thì b
- Cho hai hàm số $\Large f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+\dfrac{3}{4}$ và
- Biết $\Large \int\limits_{0}^{\dfrac{\pi }{3}}{\dfrac{{{x}^{2}}dx}{{{(