Cho hai hàm số $\Large f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+\dfrac{3}{4}$ và

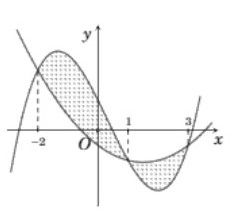
Cho hai hàm số $\Large f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+\dfrac{3}{4}$ và $\Large g(x)=d{{x}^{2}}+ex-\dfrac{3}{4}$, $\Large (a,b,c,d,e\in R)$ . Biết rằng đồ thị của hàm số $\Large y=f(x)$ và $\Large y=g(x)$ cắt nhau tại ba điểm có hoành độ lần lượt là $\Large -2;1;3$ ( tham khảo hình vẽ ) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

• A.

  $\Large \dfrac{253}{48}$

• B.

  $\Large \dfrac{125}{24}$

• C.

  $\Large \dfrac{125}{48}$

• D.

  $\Large \dfrac{253}{24}$

Phương trình hoành độ giao điểm $\Large a{{x}^{3}}+b{{x}^{2}}+cx+\frac{3}{4}=d{{x}^{2}}+ex-\dfrac{3}{4}\Rightarrow a{{x}^{3}}+(b-d){{x}^{2}}+(c-e)x+\frac{3}{2}=0$

Đặt $\Large h(x)=a{{x}^{3}}+(b-d){{x}^{2}}+(c-e)x+\dfrac{3}{2}$

Dựa vào đồ thị ta có $\Large h(x)=0$ có ba nghiệm là $\Large x=-2.x=1,x=3$

Khi đó ta có hệ: $\Large \left\{ \begin{align}  & -8a+4(b-d)-2(c-e)=-\dfrac{3}{2} \\  & a+(b-d)+(c-e)=-\dfrac{3}{2} \\  & 27a+9(b-d)+3(c-e)=-\dfrac{3}{2} \\ \end{align} \right.$ $\Large \Leftrightarrow \left\{ \begin{align}  & a=\dfrac{1}{4} \\  & b-d=-\dfrac{1}{2} \\  & c-e=-\dfrac{5}{4} \\ \end{align} \right.$

Khi đó diện tích hình phẳng cần tính là: 

$\Large S=\int\limits_{-2}^{3}{\left| f(x)-g(x) \right|dx=\int\limits_{-2}^{1}{\left| \dfrac{1}{4}{{x}^{3}}-\dfrac{1}{2}{{x}^{2}}-\dfrac{5}{4}x+\dfrac{3}{2} \right|dx+\int\limits_{1}^{3}{\left| \dfrac{1}{4}{{x}^{3}}-\dfrac{1}{2}{{x}^{2}}-\dfrac{5}{4}x+\dfrac{3}{2} \right|dx}}}$

$\Large= \int\limits_{-2}^{1}{\left( \dfrac{1}{4}{{x}^{3}}-\dfrac{1}{2}{{x}^{2}}-\dfrac{5}{4}x+\dfrac{3}{2}\right) dx - \int\limits_{1}^{3}{\left(\dfrac{1}{4}{{x}^{3}}-\dfrac{1}{2}{{x}^{2}}-\dfrac{5}{4}x+\dfrac{3}{2} \right)dx}}=\dfrac{63}{16}+\dfrac{4}{3}=\dfrac{253}{48}$

Chọn đáp án A