Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha th

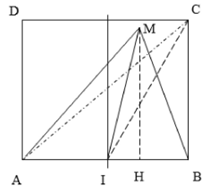
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha theo phương vuông góc với mặt chất lỏng phát ra hai sóng kết hợp với bước sóng $\Large \lambda$. Gọi C, D là hai điểm ở mặt chất lỏng sao cho ABCD là hình vuông. I là trung điểm của AB. M là một điểm nằm trong hình vuông ABCD xa I nhất mà phần tử chất lỏng tại đó dao động với biên độ cực đại và cùng pha với nguồn. Biết $\Large A B=6,6 \lambda$. Độ dài đoạn thẳng MI gần nhất giá trị nào sau đây? 

• A. $\Large 6,75 \lambda$
• B. $\Large 6,17 \lambda$
• C. $\Large 6,25 \lambda$
• D. $\Large 6,49 \lambda$

Phương pháp: 
Điều kiện có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha: $\Large d_{2}-d_{1}=k \lambda ; k \in Z$
MI là đường trung tuyến của tam giác MAB: $\Large M I^{2}=\dfrac{M A^{2}+M B^{2}}{2}-\dfrac{A B^{2}}{4}$
Cách giải: 

+ Cho $\Large \lambda=1 \Rightarrow\left\{\begin{array}{l}
A B=6,6 \\
A C=6,6 \sqrt{2}
\end{array}\right.$

+ M dao động với biên độ cực đại, cùng pha với nguồn: $\Large \left\{\begin{array}{l}
M A=k_{1} \lambda=k_{1} \\
M B=k_{2} \lambda=k_{2}
\end{array}\right.$; với  $\Large k_{1} \text { và } k_{2}$ là các số nguyên.
IC là đường trung tuyến của tam giác CAB nên: 

$\Large C I^{2}=\dfrac{A C^{2}+C B^{2}}{2}-\dfrac{A B^{2}}{4} \Rightarrow C I=\sqrt{\dfrac{6,6^{2} \cdot 2+6,6^{2}}{2}-\dfrac{6,6^{2}}{4}}=7,38$

MI là đường trung tuyến của tam giác MAB nên: $\Large M I^{2}=\dfrac{M A^{2}+M B^{2}}{2}-\dfrac{A B^{2}}{4}$
M là 1 điểm nằm trong hình vuông ABCD nên: 

+ $\Large M A < A C \Leftrightarrow k_{1} < 6,6 \sqrt{2}=9,33 \Rightarrow k_{1} \leq 9$

+ $\Large M I < C I \Leftrightarrow \dfrac{M A^{2}+M B^{2}}{2}-\dfrac{A B^{2}}{4} < B C^{2}+B I^{2}$

+ $\Large \dfrac{M A^{2}+M B^{2}}{2}-\dfrac{A B^{2}}{4} < A B^{2}+\dfrac{A B^{2}}{4} \Leftrightarrow \dfrac{M A^{2}+M B^{2}}{2} < 1,5 A B^{2}$ $\Large \Leftrightarrow \dfrac{M A^{2}+M B^{2}}{2} < 1,5.6,6^{2}$

$\Large \Rightarrow M A^{2}+M B^{2} < 130,68 \Leftrightarrow k_{1}^{2}+k_{2}^{2} < 130,68(1)$ 

+ $\Large M B^{2}+A B^{2} > M A^{2} \Rightarrow k_{2}^{2}+6,6^{2} > k_{1}^{2}(2)$

+ $\Large M H=x \Rightarrow \sqrt{M A^{2}-x^{2}}+\sqrt{M B^{2}-x^{2}}=A B \Rightarrow \sqrt{k_{1}^{2}-x^{2}}+\sqrt{k_{2}^{2}-x^{2}}=6,6(3)$

Xét các cặp $\Large k _{1} \text { và } k _{2}$ thỏa mãn (1); (2) và (3) ta tìm được: 

$\Large k_{1}=8 ; k_{2}=6 \Rightarrow M I=\sqrt{\dfrac{8^{2}+6^{2}}{2}-\dfrac{6,6^{2}}{4}}=6,2537$

Chọn C