Một con lắc lò xo treo thẳng đứng dao động điều hòa theo phương thẳng

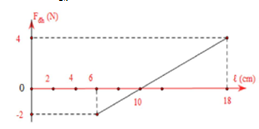
Một con lắc lò xo treo thẳng đứng dao động điều hòa theo phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc lực đàn hồi của lò xo $\Large F_{d k}$ vào chiều dài $\Large l$ của lò xo. Độ dãn của lò xo tại vị trí cân bằng là

• A. 4 cm
• B. 6 cm
• C. 8 cm
• D. 2 cm

Phương pháp: 
Lực đàn hồi = (độ cứng).(độ biến dạng) 
Chiều dài cực đại và cực tiểu của lò xo: 
Cách giải: 
Fdh biến thiên từ - 2N đến 4N $\Large \Rightarrow$ trong quá trình dao động lò xo có thể bị nén, bị dãn và có chiều dài tự nhiên. 
Khi lò xo bị nén cực đại, $\Large F_{\text {dhn }}=k\left(A-\Delta l_{0}\right)=2 N$ lò xo có chiều dài $\Large l_{\min }=6 cm$
Khi $\Large F_{d h}=0$ lò xo có chiều dài tự nhiên $\Large l_{0}=10 cm$

Khi lò xo bị dãn cực $\Large \left\{\begin{array}{l}
l_{\max }=l_{c b}+A \\
l_{\min }=l_{c b}-A
\end{array}\right.$ đại, $\Large F_{dhd}=k\left(A+\Delta l_{0}\right)=4$ lò xo có chiều dài $\Large l_{\max }=18 cm$

$\Large \left\{\begin{array}{l}
l_{\text {max}}=l_{c b}+A \\
l_{\min }=l_{c b}-A
\end{array} \Rightarrow A=\dfrac{l_{\max }-l_{\min }}{2}=\dfrac{18-6}{2}=6 cm \right.$

$\Large \Rightarrow \dfrac{F_{\text {dhd }}}{F_{\text {dhn }}}=\dfrac{A+\Delta_{0}}{A-\Delta_{0}}=\dfrac{4}{2}=2 \Leftrightarrow \dfrac{6+\Delta l_{0}}{6-\Delta l_{0}}=2 \Rightarrow \Delta l_{0}=2 cm$

Chọn D