Đặt điện áp xoay chiều $\Large u=U \sqrt{2} \cos (2 \pi f t) V$ (f tha

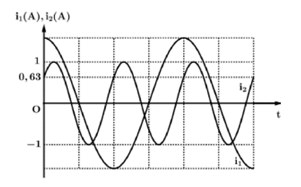
Đặt điện áp xoay chiều $\Large u=U \sqrt{2} \cos (2 \pi f t) V$ (f thay đổi được) vào hai đầu đoạn mạch AB gồm cuộn dây có điện trở r, tụ điện và điện trở R theo thứ tự mắc nối tiếp. Biết $\Large R \leq r_{,} N$ là điểm nối giữa cuộn dây và tụ điện. Với $\Large f=f_{1}$ thì cường độ dòng điện trong mạch là  $\Large i_{1}$ và công suất tiêu thụ của đoạn NB là $\Large P _{1}$, nếu đặt điện áp trên với tần số $\Large f_{1}$ vào hai đầu R thì công suất tiêu thụ của R là $\Large 4P _{1}$. Với $\Large f=f_{2}$ thì cường độ dòng điện trong đoạn mạch AB ban đầu là i2. Đồ thị biểu diễn sự phụ thuộc của $\Large i_{1}$ và $\Large i_{2}$ theo thời gian t như hình vẽ. Cường độ hiệu dụng của dòng điện $\Large i_{1}$ là 

• A. 1,12 A
• B. 1,62 A
• C. 1,23 A
• D. 1,58 A

Phương pháp: 
Sử dụng các công thức của mạch R, L, C mắc nối tiếp kết hợp với kĩ năng đọc đồ thị. 
Cách giải: 
Ta có: $\Large u=U \sqrt{2} \cos (2 \pi f t) V$
+ Khi $\Large f=f_{1}$ từ đồ thị ta có: $\Large i=I_{01} \cdot \cos (2 \pi f t)(A)$
$\Large \Rightarrow \varphi_{1}=0 \Rightarrow i_{1}$ cùng pha với $\Large u \Rightarrow Z_{1}=R+r$
+ Khi $\Large f=f_{2}$ từ đồ thị ta có: $\Large \cos \varphi_{2}=\dfrac{0,63}{1}=0,63=\dfrac{R+r}{Z_{2}}=\dfrac{Z_{1}}{Z_{2}}$
Có $\Large I_{0}=\dfrac{U_{0}}{Z} \Rightarrow \dfrac{I_{01}}{I_{02}}=\dfrac{Z_{2}}{Z_{1}}=\dfrac{1}{0,63}$ $\Large \Rightarrow I_{01}=\dfrac{I_{02}}{0,63}=\dfrac{1}{0,63}=1,5873 A \Rightarrow I_{1}=1,12 A$
Chọn A.