Một nguồn âm P phát ra âm đẳng hướng. Hai điểm A, B nằm cùng trên một

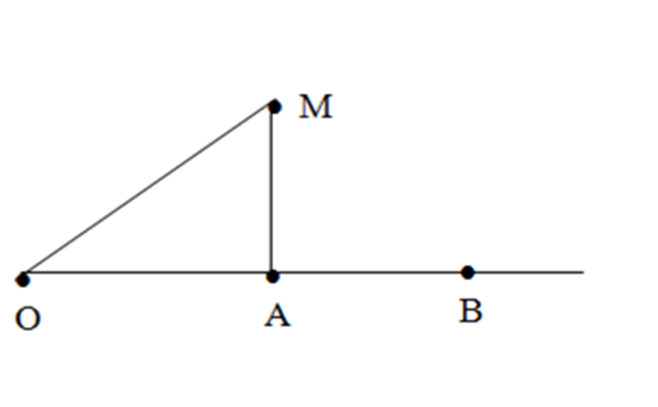
Một nguồn âm P phát ra âm đẳng hướng. Hai điểm A, B nằm cùng trên một phương truyền sóng có mức cường độ âm lần lượt là 40 dB và 30 dB. Điểm M nằm trong môi trường truyền sóng sao cho ∆AMB vuông cân ở A. Xác định mức cường độ âm tại M?

• A. A. 37,54 dB
• B. B. 32,46 dB
• C. C. 35,54 dB
• D. D. 38,46 dB

Chọn B

Gọi P là công suất nguồn âm

OA=R; OB= ${{R}_{B}}$=R+r ; AB=AM=r ; OM=${{R}_{M}}$

${{R}_{M}}^{2}={{R}^{2}}+{{r}^{2}}(*)$

${{L}_{A}}=10\lg \frac{{{I}_{A}}}{{{I}_{0}}};{{L}_{B}}=10\lg \frac{{{I}_{B}}}{{{I}_{0}}};{{L}_{M}}=10\lg \frac{{{I}_{M}}}{{{I}_{0}}}$

Với $I=\frac{P}{4\pi {{R}^{2}}}$

${{L}_{A}}-{{L}_{B}}=10\lg \frac{{{I}_{A}}}{{{I}_{0}}}-10\lg \frac{{{I}_{B}}}{{{I}_{0}}}=10\lg \frac{{{I}_{A}}}{{{I}_{B}}}=10\lg \frac{{{R}_{B}}^{2}}{{{R}_{A}}^{2}}$.

${{L}_{A}}-{{L}_{B}}=10dB=>10\lg \frac{{{R}_{B}}^{2}}{{{R}_{A}}^{2}}=10=>\frac{{{R}_{B}}^{2}}{{{R}_{A}}^{2}}=10=>{{R}_{B}}^{2}=10{{R}_{A}}^{2}$
 

${{(R+r)}^{2}}=10{{R}^{2}}=>{{r}^{2}}+2rR-9{{R}^{2}}=0=>r=R(\sqrt{10}-1)(**)$

${{R}_{M}}^{2}={{R}^{2}}+{{r}^{2}}={{R}^{2}}(12-2\sqrt{10})$

${{L}_{A}}-{{L}_{M}}=10\lg \frac{{{R}_{M}}^{2}}{{{R}_{A}}^{2}}=10\lg \frac{{{R}_{M}}^{2}}{{{R}^{2}}}=10\lg (12-2\sqrt{10})=7,54dB$

${{L}_{M}}={{L}_{A}}-7,54=32,46dB$