Một mạch điện gồm R nối tiếp tụ điện C nối tiếp cuộn L. Duy trì hai đầ

Một mạch điện gồm R nối tiếp tụ điện C nối tiếp cuộn L. Duy trì hai đầu đoạn mạch một điện áp xoay chiều $\Large u=240\sqrt{2}cos(100\pi t) (V),$ điện trở có thể thay đổi được. Cho $\Large R=80\Omega; I=\sqrt{3}A, U_{CL}=80\sqrt{3} V,$ điện áp $\Large u_{RC}$ vuông pha với $\Large u_{CL}.$ Tính L?

 

• A.

  A. 0,37H

• B.

  B. 0,58H

• C.

  C. 0,68H

• D.

  D. 0,47H

Ta có $\Large U=240(V); U_{R}=IR=80\sqrt{3}\ (V)$

Vẽ giản đồ véctơ như hình vẽ:

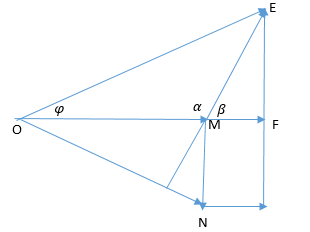
$\Large U_{R}=U_{LC}=80\sqrt{3}  V.$ Xét tam giác cân OME
$\Large U^{2}=U_{R}^{2}+U_{CL}^{2}-2U_{R}U_{L}cos\alpha \Rightarrow \alpha=\dfrac{2\pi}{3}$
$\Large \Rightarrow \beta =\dfrac{\pi}{3}\Rightarrow \varphi =\dfrac{\pi}{6}$
Xét tam giác OMN: $\Large U_{C}=U_{R}tan\varphi =80(V)\ (1)$
Xét tam giác OEF: $\Large EF=OEsin\varphi$
$\Large U_{L}-U_{C}=Usin\dfrac{\pi}{6}=120(V)\ (2).$ Từ (1) và (2) suy ra $\Large U_{L}=200(V)$
Do đó $\Large Z_{L}=\dfrac{U_{L}}{I}=\dfrac{200}{\sqrt{3}}\Rightarrow L=\dfrac{Z_{L}}{100\pi}=\dfrac{200}{100\pi\sqrt{3}}=0,3677\ H\approx 0,37\ H.$

Chọn đáp án A