Một học sinh xác định điện dung của tụ điện bằng cách đặt điện áp $\La

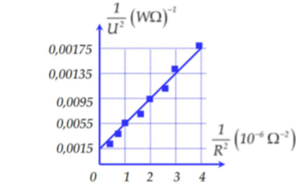
Một học sinh xác định điện dung của tụ điện bằng cách đặt điện áp $\Large u=U_0.cos\omega t$ ($\Large U_0$ không đổi, $\Large \omega =3,14 rad/s$) vào hai đầu một đoạn mạch gồm tụ điện có điện dung C mắc nối tiếp với biến trở R. Biết $\Large \dfrac{1}{U^2}=\dfrac{2}{U_0^2}+\dfrac{2}{U_0^2.\omega^2.C^2}.\dfrac{1}{R^2};$ trong đó điện áp U giữa hai đầu R được đo bằng đồng hồ đo điện đa năng hiện số. Dựa vào kết quả thực nghiệm đo được trên hình vẽ, học sinh này tính được giá trị của C là:

• A.

  $\Large 5,20.10^{-6}F.$

• B.

  $\Large 1,95.10^{-6}F.$

• C.

  $\Large 1,95.10^{-3}F.$

• D.

  $\Large 5,20.10^{-3}F.$

Phương pháp:

Sử dụng các vị trí tại $\Large \dfrac{1}{R^2}=1$ thì $\Large \dfrac{1}{U^2}=0,0055$ và tại $\Large \dfrac{1}{R^2}=2$ thì $\Large \dfrac{1}{U^2}=0,0095$ ta tìm được C.

Cách giải:

+ Tại $\Large \dfrac{1}{R^2}=10^{-6}$ thì $\Large \dfrac{1}{U^2}=0,0055$ ta có:

$\Large \dfrac{1}{U^2}=\dfrac{2}{U_0^2}+\dfrac{2}{U_0^2.\omega^2.C^2}.\dfrac{1}{R^2} \Leftrightarrow 0,0055=\dfrac{2}{U_0^2}+\dfrac{2.10^{-6}}{U_0^2.\omega^2.C^2}$

+ Tại $\Large \dfrac{1}{R^2}=2.10^{-6}$ thì $\Large \dfrac{1}{U^2}=0,0095$ ta có:

$\Large \dfrac{1}{U^2}=\dfrac{2}{U_0^2}+\dfrac{2}{U_0^2.\omega^2.C^2}.\dfrac{1}{R^2} \Leftrightarrow 0,0095=\dfrac{2}{U_0^2}+\dfrac{4.10^{-6}}{U_0^2.\omega^2.C^2}$

Ta được hệ phương trình:

$\Large \left\{\begin{align} & 0,0055=\dfrac{2}{U_0^2}+\dfrac{2}{U_0^2.\omega^2.C^2}.10^{-6} \\ &0,0095=\dfrac{2}{U_0^2}+\dfrac{4}{U_0^2.\omega^2.C^2}.10^{-6} \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & 0,0055=\dfrac{2}{U_0^2}\left(1+\dfrac{2}{3,14^2.C^2}.10^{-6}\right) \ (1) \\ & 0,0095=\dfrac{2}{U_0^2}\left(1+\dfrac{2}{3,14^2.C^2}.2.10^{-6}\right) \ (2) \end{align}\right.$

Lấy (2) chia (1) ta được: $\Large C=1,95.10^{-6}F$

Chọn B.