Hai nguồn phát sóng kết hợp tại A, B trên mặt nước cách nhau 12cm phát

Hai nguồn phát sóng kết hợp tại A, B trên mặt nước cách nhau 12cm phát ra hai dao động điều hòa cùng tần số 20Hz, cùng biên độ và cùng pha ban đầu. Xét điểm M trên mặt nước cách A, B những đoạn lần lượt là 4,2cm và 9cm. Tốc độ truyền sóng trên mặt nước là 32cm/s. Muốn M là một điểm dao động với biên độ cực tiểu thì phải dịch chuyển nguồn tại B dọc đường nối A, B từ vị trí ban đầu ra xa nguồn A một đoạn nhỏ nhất là

• A. 0,53 cm.
• B. 1,03 cm.
• C. 0,23 cm.
• D. 0,83 cm.

Phương pháp:
Bước sóng: $\Large \lambda=\dfrac{v}{f}$
Điều kiện có cực đại giao thoa: $\Large d_2-d_1=k\lambda; k\in Z$
Điều kiện có cực tiểu giao thoa: $\Large d_2-d_1=\left(k+\dfrac{1}{2}\right)\lambda; k \in Z$
Vẽ hình, sử dụng các định lí toán học: hàm số cos, định lí Pitago,.. 
Cách giải:
Bước sóng: $\Large \lambda=\dfrac{v}{f}=\dfrac{32}{20}=1,6cm$
Xét tỷ số: $\Large \dfrac{d_2-d_1}{\lambda}=\dfrac{9-4,2}{1,6}=3$
Vậy ban đầu M nằm trên cực đại bậc 3. 
Dịch chuyển B ra xa một đoạn $\Large \Delta d,$ để đoạn này là nhỏ nhất thì khi đó M phải nằm trên cực tiểu thứ 4 với:
$\Large {d_2}'-d_1=\left(3+\dfrac{1}{2}\right)\lambda=3,5\lambda=3,5.1,6=5,6 cm \Rightarrow {d_2}'=9,8 cm$

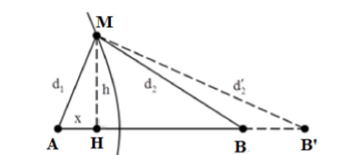
Áp dụng định lí hàm số cos cho tam giác MAB ta có: $\Large MB^2=MA^2+AB^2-2AM.AB.cosA$
$\Large cosA=\dfrac{MA^2+AB^2-MB^2}{2AM.AB}=\dfrac{4,2^2+12^2-9^2}{2.4,2.12}=0,8$ $\Large \Rightarrow \left\{\begin{align} & AH=AM.cosA=4,2.0,8=3,36 cm \\ & MH=AM.sinA=4,2.0,6=2,52 cm \end{align}\right.$    
Áp dụng định lý Pitago trong tam giác vuông MHB’ ta có: $\Large {HB}'=\sqrt{{MB}'^2-MH^2}=\sqrt{9,8^2-2,52^2}=9,47 cm$
Đoạn dịch chuyển: $\Large {BB}'={HB}'-HB={HB}'-(AB-AH)=9,47-(12-3,36)=0,83 cm$
Chọn D.