Một hình trụ có diện tích xung quanh là $\large 4\pi$, thiết diện qua

Một hình trụ có diện tích xung quanh là $\large 4\pi$, thiết diện qua trục là hình vuông. Một mặt phẳng $\large (\alpha )$ song song với trục, cắt hình trụ theo thiết diện ABB'A', biết một cạnh của thiết diện là một dây của đường tròn đáy hình trụ và căng một cung $\large 120^{\circ}$. Diện tích thiết diện ABB'A' là:  

• A. A. $\large \sqrt{3}$
• B. B. $\large 2\sqrt{3}$
• C. C. $\large 2\sqrt{2}$
• D. D. $\large 3\sqrt{2}$

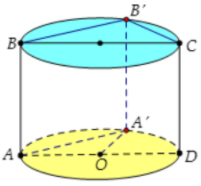
Thiết diện qua trục là hình vuông nên: h = AB = AD = 2R.

$\large \Rightarrow S_{xq} = 2\pi Rh = 2\pi R.2R = 4\pi R^{2} \Rightarrow OA = R = \sqrt{\dfrac{S_{xq}}{4\pi }} = \sqrt{\dfrac{4\pi }{4\pi }} = 1$.

Suy ra AB = 2. Ta có: 

$\large \widehat{AOA'} = 120^{\circ} \Rightarrow AA'^{2} = OA^{2} + OA'^{2} - 2OA.OA'.cos120^{\circ}$ 

$\large = 1^{2}+1^{2}-2.1.1.\left ( \dfrac{-1}{2} \right ) = 3$ $\large \Rightarrow AA' = \sqrt{3}$ 

Suy ra diện tích hình chữ nhật ABB'A' là: AB.AA' = $\large 2\sqrt{3}$.