Hai vật $ M_{1}$ và $ M_{2}$ dao động điều hòa với li độ lần lượt là $

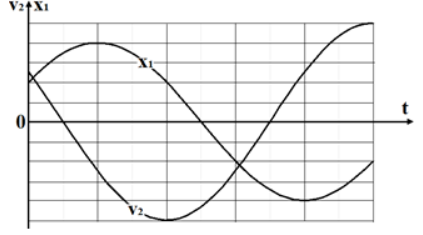
Hai vật $ M_{1}$ và $ M_{2}$ dao động điều hòa với li độ lần lượt là $ x_{1} = A_{1}cos(\omega_{1}t + \varphi_{1})$ và $ x_{2} = A_{2}cos(\omega_{2}t + \varphi_{2})$. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ $ x_{1}$ của $ M_{1}$ và vận tốc $ v_{2}$ của $ M_{2}$ theo thời gian t. Giá trị của $ sin(\varphi_{1} - \varphi_{2})$ gần giá trị nào nhất sau đây?

• A. -0,71.
• B. -0,49.
• C. 0,87.
• D. 0,49.

Hướng dẫn:

+ Xét tại thời điểm mà $ x_{1} = +\dfrac{A}{2}$ và đang đi xuống (đang giảm) thì $ v_{2}$ đạt lớn nhất và âm.

Suy ra $ x_{2} = 0$ và đang đi về biên âm.

$ \left\{\begin{array}{l} \varphi_{1} = \dfrac{\pi}{3} \\ \varphi_{2} = \dfrac{\pi}{2} \end{array}\right. \rightarrow sin(\varphi_{1}-\varphi_{2}) = -0,5 \approx -0,49$