Hai quả cầu kim loại nhỏ, giống hệt nhau, chứa các điện tích cùng dấu

Hai quả cầu kim loại nhỏ, giống hệt nhau, chứa các điện tích cùng dấu $\Large q_1$ và $\Large q_2$, được treo vào chung một điểm O bằng hai sợi dây chỉ mảnh, không dãn, dài bằng nhau. Hai quả cầu đẩy nhau và góc giữa hai dây treo bằng $\Large 60^{\circ}$. Cho hai quả cầu tiếp xúc với nhau, rồi thả ra thì chúng đẩy nhau mạnh hơn và góc giữa hai dây treo bây giờ là $\Large 80^{\circ}$. Tỉ số $\Large q_1/q_2$ có thể là

• A. 7,5.
• B. 0,085.
• C. 10.
• D. 9.

Chọn A.

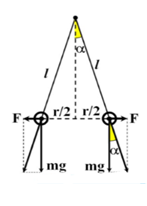
Hệ cân bằng lúc đầu: $\Large tan\alpha =\dfrac{F}{mg}=\dfrac{kq_1q_2}{mgr^2}=\dfrac{kq_1q_2}{mg(2lsin\alpha)^2}$

Hệ cân bằng sau đó: $\Large tan\alpha'=\dfrac{F}{mg}=\dfrac{k\left(\dfrac{q_1+q_2}{2}\right)^2}{mg(2lsin\alpha')^2}$

$\Large \dfrac{tan\alpha'}{tan\alpha}\left(\dfrac{sin\alpha'}{sin\alpha}\right)^2$ $\Large =\dfrac{1}{4}\left(\dfrac{q_1}{q_2}+\dfrac{q_2}{q_1}+2\right)$ $\Large \xrightarrow[\alpha'=40^{\circ}]{\alpha=30^{\circ}}$ $\Large \left[\begin{align} & \dfrac{q_1}{q_2}=7,5 \\ & \dfrac{q_1}{q_2}=0,13 \end{align}\right.$.