Hai dao động điều hòa cùng phương, cùng tần số có phương trình lần lượ
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Hai dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là và Dao động tổng hợp có biên độ Để biên độ có giá trị cực đại thì phải có giá trị là
Đáp án án đúng là: C
Lời giải chi tiết:
Phương pháp:
+ Sử dụng giản đồ Fresnen
+ Áp dụng định lí hàm số sin:
Cách giải:
Ta có:
và biên độ dao động tổng hợp
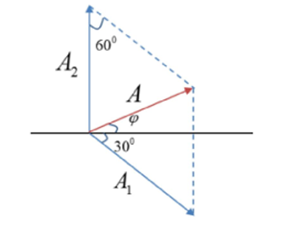
Để thì
Khi đó:
Chọn C.
Xem thêm các bài tiếp theo bên dưới