Hai con lắc lò xo A và B giống nhau, dao động trên hai đường thẳng son

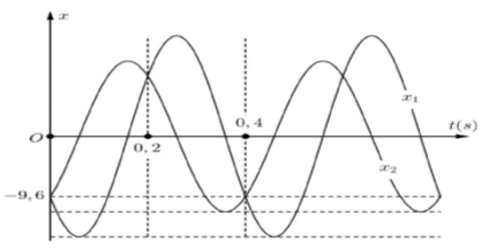
Hai con lắc lò xo A và B giống nhau, dao động trên hai đường thẳng song song, gần nhau và dọc theo trục Ox. Vị trí cân bằng của hai con lắc cùng nằm trên một đường thẳng vuông góc với trục Ox tại O. Hình bên là đồ thị của li độ dao động của con lắc A (đường 1) và của con lắc B (đường 2) phụ thuộc vào thời gian t. Mốc thế năng tại vị trí cân bằng của mỗi vật. Lấy $\Large \pi^{2}=10$. Biết khoảng cách giữa hai vật của hai con lắc dọc theo trục Ox có giá trị lớn nhất là 20 cm. Khi động năng con lắc A là 0,24 J thì thế năng con lắc B là

• A. 90 mJ
• B. 240 mJ
• C. 150 mJ
• D. 135 mJ

Phương pháp:
Từ đồ thị ta thấy $\Large x_1,x_2$ vuông pha. 
Khoảng cách giữa hai vật của hai con lắc dọc theo trục Ox trong quá trình dao động được xác định bởi phương trình: $\Large d=|x_1-x_2|=A.\cos(\omega t+\varphi)\Rightarrow d_{max}=A$ 
Sử dụng lí thuyết về tổng hợp dao động kết hợp kĩ năng đọc đồ thị và VTLG.
Biểu thức của động năng và thế năng: $\Large \left\{\begin{align}&W_d=\dfrac{1}{2}mv^{2}=\dfrac{1}{2}m\omega^{2}.A^{2}\sin^{2}(\omega t+\varphi)\\&W_t=\dfrac{1}{2}kx^{2}=\dfrac{1}{2}m\omega^{2}A^{2}\cos^{2}(\omega t+\varphi)\\\end{align}\right.$
Cách giải:
Giả sử phương trình dao động của hai vật có dạng: $\Large \left\{\begin{align}&x_1=A_1\cos(\omega t+\varphi_1)\\&x_2=A_2\cos(\omega t+\varphi_2)\\\end{align}\right.$

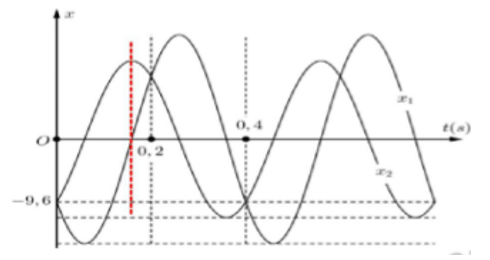
+ Từ đồ thị ta thấy khi $\Large x_{2max}=A_2$ thì $\Large x_1=0\Rightarrow x_1,x_2$ vuông pha. 
Khoảng cách giữa hai vật của hai con lắc dọc theo trục Ox trong quá trình dao động được xác định bởi phương trình: $\Large d=|x_1-x_2|=A\cos(\omega t+varphi)\Rightarrow d_{max}=A$
Với: $\Large A=\sqrt{A_1^{2}+A_2^{2}}$ (do $\Large x_1,x_2$ vuông pha) 
Khoảng cách này có giá trị lớn nhất là 20cm $\Large d_{max}=A=20cm\Rightarrow A_1^{2}+A_2^{2}=20^{2}(1)$  
+ Từ đồ thị ta thấy tại t = 0 hai vật có cùng li độ $\Large x_1=x_2=-9,6$
Biểu diễn trên VTLG ta có:
 
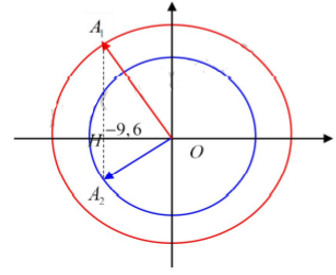
Tam giác $\Large OA_1A_2$ vuông tại O có đường cao OH. Áp dụng hệ thức lượng trong tam giác ta có:
$\Large \dfrac{1}{OA_1^{2}}+\dfrac{1}{OA^{2}}=\dfrac{1}{OH^{2}}\Leftrightarrow \dfrac{1}{A_1^{2}}+\dfrac{1}{A_2^{2}}=\dfrac{1}{9,6^{2}}(2)$
Từ (1) và (2) suy ra: $\Large \left\{\begin{align}&A_1=16cm\\&A_2=12cm\\\end{align}\right.$
Biểu thức xác định động năng con lắc A và thế năng con lắc B: $\Large \left\{\begin{align}&W_d=\dfrac{1}{2}mv_A^{2}=\dfrac{1}{2}m\omega^{2}A_1^{2}.\sin^{2}(\omega t+\varphi_1)\\&W_t=\dfrac{1}{2}kx_B^{2}=\dfrac{1}{2}m\omega^{2}.A_2^{2}\cos^{2}(\omega t+\varphi_2)\\\end{align}\right.$
Do $\Large x_1,x_2$ vuông pha nên: $\Large \sin^{2}(\omega t+\varphi)=\cos^{2}(\omega t+\varphi_2)$  
 $\Large \Rightarrow \dfrac{W_{dA}}{W_{tB}}=\dfrac{A_1^{2}}{A_2^{2}}\Leftrightarrow \dfrac{0,24}{W_{tB}}=\dfrac{16^{2}}{12^{2}}\Rightarrow W_{tB}=0,135J=135mJ$