Gọi Sxq là diện tích xung quanh của hình nón được sinh ra
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
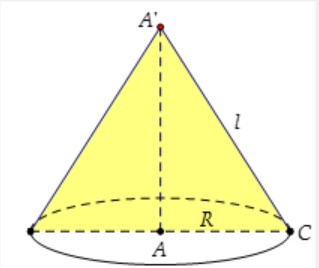
Gọi Sxq là diện tích xung quanh của hình nón được sinh ra bởi đoạn thẳng A’C của hình lập phương ABCD.A’B’C’D’ có cạnh bằng a khi quay xung quanh trục AA’. Tính diện tích Sxq.
Đáp án án đúng là: D
Lời giải chi tiết:
Ta có: R=AC=a√2. Suy ra:
l=A′C=√AA′2+AC2=√a2+(a√2)2=a√3
Khi đó diện tích xung quanh của hình nón là:
Sxq=πRl=π.a√2.a√3=πa2√6
Xem thêm các bài tiếp theo bên dưới
- Cho tứ diện đều ABCD có cạnh bằng 3 a . Hình nón ( N ) có đỉnh A và đư
- Cho hình nón đỉnh S có chiều cao h = a và bán kính đáy r = 2a . Mặt ph
- Cho một khối trụ có bán kính đường tròn đáy bằng 6. Cắt khối trụ bởi m
- Một hình trụ tròn xoay bán kính R = 1. Trên đường tròn ( O ) và ( O’ )
- Tính bán kính mặt cầu tiếp xúc với tất cả các cạnh của một hình lập ph