Cho tứ diện đều ABCD có cạnh bằng 3 a . Hình nón ( N ) có đỉnh A và đư
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
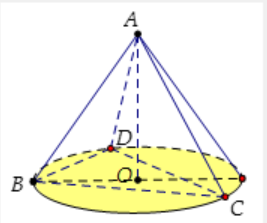
Cho tứ diện đều ABCD có cạnh bằng 3a. Hình nón (N) có đỉnh A và đường tròn đáy là đường tròn ngoại tiếp tam giác BCD. Tính diện tích xung quanh $\large S_{xq}$ của hình nón (N).
Đáp án án đúng là: B
Lời giải chi tiết:
Do BCD là tam giác đều cạnh 3a $\large \Rightarrow R = OB = \dfrac{3a\sqrt{3}}{3} = a\sqrt{3}$
Ta có độ dài đường sinh l = AB = 3a. Suy ra:
$\large S_{xq} = \pi Rl = \pi .a\sqrt{3}.3a = 3\sqrt{3}\pi a^{2}$
Xem thêm các bài tiếp theo bên dưới
- Cho hình nón đỉnh S có chiều cao h = a và bán kính đáy r = 2a . Mặt ph
- Cho một khối trụ có bán kính đường tròn đáy bằng 6. Cắt khối trụ bởi m
- Một hình trụ tròn xoay bán kính R = 1. Trên đường tròn ( O ) và ( O’ )
- Tính bán kính mặt cầu tiếp xúc với tất cả các cạnh của một hình lập ph
- Gọi r và h lần lượt bán kính đáy và chiều cao của một hình nón. Kí hiệ