Đồ thị của hàm só $\large y=3 x^{4}-4 x^{3}-6 x^{2}+12 x+1$ đạt cực ti

Đồ thị của hàm só $\large y=3 x^{4}-4 x^{3}-6 x^{2}+12 x+1$ đạt cực tiểu tại $\large M\left(x_{1} ; y_{1}\right)$. Tính tổng $\large-2 (x_{1})^2+(y_{1})^3$

• A.

  A. 700

• B.

  B. 998

• C.

  C. 1000

• D.

  D. 900

Chọn B

Ta có: $\large y^{\prime}=12 x^{3}-12 x^{2}-12 x+12$

$\large y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l}
x=1 \Rightarrow y=6 \\
x=-1 \Rightarrow y=-10
\end{array}\right.$

Bảng biến thiên:

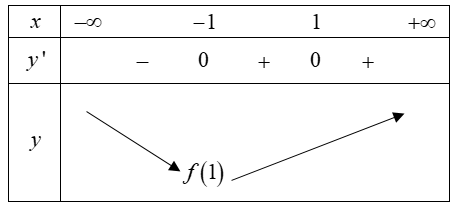
Dựa vào bảng biến thiên suy ra hàm số đạt cực tiểu tại $\large \Rightarrow M(-1 ;-10) \Rightarrow -2 (x_{1})^2+(y_{1})^3=998$