Đặt điện áp $ u=U_{0}.cos \omega t$($ U_{0}, \omega$ không đổi) vào đo

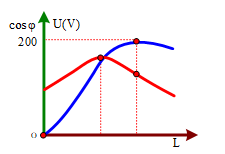
Đặt điện áp $ u=U_{0}.cos \omega t$($ U_{0}, \omega$ không đổi) vào đoạn mạch mắc nối tiếp gồm điện trở R, tụ điện có điện dung C và cuộn cảm thuần có độ tự cảm L thay đổi. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng UL­ giữa hai đầu cuộn cảm và hệ số công suất $ cos \varphi$ của đoạn mạch theo giá trị của độ tự cảm L. Giá trị của $ U_{0}$ gần nhất với giá trị nào sau đây?

• A. A. 240V.
• B. B. 165V.
• C. C. 220V.
• D. D. 185V.

Hướng dẫn:

Khi xảy ra cực đại của điện áp hiệu dụng trên cuộn cảm thuần $ Z_{L}=\dfrac{R^{2}+Z_{C}^{2}}{Z_{C}}$

Ta chuẩn hóa $ \left\{\begin{array}{l} R=1 \\ Z_{C}=n \end{array}\right. \rightarrow Z_{L}=\dfrac{1}{x}+x$

Hệ số công suất mạch tương ứng $ cos \varphi = \dfrac{R}{\sqrt{R^{2}+(Z_{L}-Z_{C})^{2}}} \leftrightarrow 0,8=\dfrac{1}{\sqrt{1+\dfrac{1}{n^{2}}}} \rightarrow n=\dfrac{4}{3}$

Kết hợp với

$ U_{Lmax}= U \sqrt{1+(\dfrac{Z_{C}}{R})^{2}} \rightarrow U=\dfrac{U_{Lmax}}{\sqrt{1+(\dfrac{Z_{C}}{R})^{2}}}=\dfrac{U_{Lmax}}{\sqrt{1+(\dfrac{4}{3})^{2}}}=120V \rightarrow U_{0}=120 \sqrt{2} \approx 170V$