Một sóng hình sin lan truyền trên mặt nước từ nguồn O với bước sóng $

Một sóng hình sin lan truyền trên mặt nước từ nguồn O với bước sóng $ \lambda$.Ba điểm A, B, C trên hai phương truyền sóng sao cho OA vuông góc với OC và B là một điểm thuộc tia OA sao cho OB > OA. Biết $ OA=7 \lambda$. Tại thời điểm người ta quan sát thấy giữa A và B có 5 đỉnh sóng (kể cả A và B) và lúc này góc $ \widehat{ACB}$ đạt giá trị lớn nhất. Số điểm dao động ngược pha với nguồn trên đoạn AC bằng

• A. 4.
• B. 5.
• C. 6.
• D. 7.

Hướng dẫn:

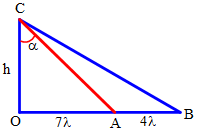
Giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng $ \rightarrow AB=4 \lambda$. Chuẩn hóa $ \lambda=1$.

Ta có: $ \left\{\begin{array}{l} tan \alpha = \dfrac{7 \lambda}{h} \\ tan \beta \dfrac{11 \lambda}{h} \end{array}\right. \rightarrow tan(\beta - \alpha)=tan C=\dfrac{\dfrac{4 \lambda}{h}}{1+\dfrac{77 \lambda^{2}}{h^{2}}}=\dfrac{4 \lambda}{h+\dfrac{77\lambda^{2}}{h^{2}}}$

Từ biểu thức trên ta thấy góc $ \widehat{ACB}$ lớn nhất khi $ h=\sqrt{77}$.

Gọi M là một điểm trên AC, để M ngược pha với nguồn thì $ \dfrac{2 \pi d_{M}}{\lambda}=(2k+1)\pi \rightarrow d_{M}=(2k+1).0,5.

Với khoảng giá trị tính về phía C từ đường vuông góc của O lên AC: $ 5,47 \leq d_{M} \leq 8,7$, kết hợp với chức năng Mode $ \rightarrow 7$  ta tìm được 4 vị trí.

Tương tự như vậy, ta xét đoạn về phía A: $ 5,47 \leq d_{M} \leq 7$ ta tìm được 2 vị trí

$ \rightarrow$ Trên AC có 6 vị trí.