Cho x, y là các số thực dương thỏa mãn điều kiện $\Large 5^{x+4y}+\dfr

Cho x, y là các số thực dương thỏa mãn điều kiện $\Large 5^{x+4y}+\dfrac{3}{3^{xy}}+x+1=\dfrac{5^{xy}}{5}+3^{-x-4y}+y(x-4)$. Tìm giá trị nhỏ nhất của biểu thức P = x+ y 

 

• A.

  A. $\Large 3$

• B.

  B. $\Large 5+2\sqrt{5}$

• C.

  C. $\Large 3-2\sqrt{5}$

• D.

  D. $\Large 1+\sqrt{5}$

Chọn B

Ta có:

$\Large \begin{align}5^{x+4y}+\dfrac{3}{3^{xy}}+x+1=\dfrac{5^{xy}}{5}+3^{-x-4y}+y(x-4)\\\Leftrightarrow 5^{x+4y}-3^{-x-4y}+x+4y=5^{xy-1}-3^{1-xy}+xy-1 (1)\end{align}$

Xét hàm số: $\Large f(t)=5^t-3^{-t}+t$ trên $\Large \mathbb{R}$

Vì: $\Large f'(t)=5^t.\ln5+3^{-t}.\ln3+1>0; \forall x\in\mathbb{R}$ nên hàm số f(t) đồng biến trên $\Large \mathbb{R}$ (2)

Từ (1) và (2) ta có: $\Large x+4y=xy-1$ (3). Dễ thấy x =4 không thỏa mãn (3)

Với $\Large x\neq4, (3)\Leftrightarrow y=\dfrac{x+1}{x-4}$ kết hợp điều kiện $\Large x, y > 0$ suy ra $\Large x > 4$

Do đó $\Large P=x+y=x+\dfrac{x+1}{x-4}$

Xét hàm số $\Large g(x)=x+\dfrac{x+1}{x-4}$ trên $\Large (4; +\infty)$

Ta có: $\Large g'(x)=1-\dfrac{5}{(x-4)^2}=0$ $\Large \Leftrightarrow \left[\begin{align}&x=4+\sqrt{5}\\&x=4-\sqrt{5}\\\end{align}\right.$

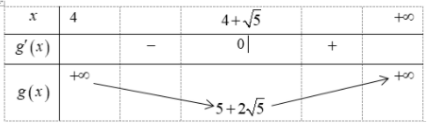
Dựa vào bảng biến thiên ta có $\Large P \underset{(4; +\infty)}{min}(x)=5+2\sqrt{5}$