Cho tứ diện đều SABC cạnh a . Gọi M , N lần lượt là trung điểm của các

Cho tứ diện đều SABC cạnh a . Gọi M , N lần lượt là trung điểm của các cạnh AB, SC. Tính tan của góc giữa đường thẳng MN và mặt phẳng (ABC)
 

• A.

  $\large \dfrac {\sqrt {3}}{2}$

• B.

  $\large \dfrac {1}{2}$

• C.

  $\large \dfrac {\sqrt {2}}{2}$

• D.

  1

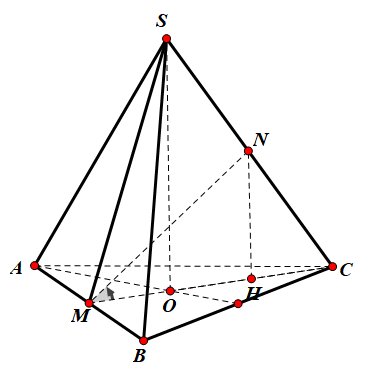
Gọi O  là tâm đường tròn ngoại tiếp đáy.
Vì SABC  là tứ diện đều cạnh a  nên $\large h = \dfrac {\sqrt {6}}{3}$
Gọi H là chân đường vuông góc từ N xuống (ABC) $\large \Rightarrow $ H là trung điểm của OC
$\large \Rightarrow MH = \dfrac {2}{3} MC = \dfrac {2}{3} \sqrt {a^{2} - (\dfrac {a}{2})^{2}} = \dfrac {\sqrt {3}}{3}a$
Vì N là trung điểm của SC nên $\large NH = \dfrac {1}{2}h = \dfrac {\sqrt {6}}{6}a$
Góc giữa đường thẳng MN và mặt phẳng  (ABC) là $\large \widehat{NMH}$
Vậy $\large \tan  \widehat{NMH} = \dfrac {NH}{MH} = (\dfrac {\sqrt {6}}{6}a) : (\dfrac {\sqrt {3}}{6}a) = \dfrac {\sqrt {2}}{2}$