Cho tam giác ABC vuông cân tại điểm A và BC = a. Trên đường thẳng qua
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho tam giác ABC vuông cân tại điểm A và BC = a. Trên đường thẳng qua A vuông góc với mặt phẳng (ABC) lấy điểm S sao cho SA=a√62. Tính số đo góc giữa đường thẳng SB và (ABC)
Đáp án án đúng là: C
Lời giải chi tiết:
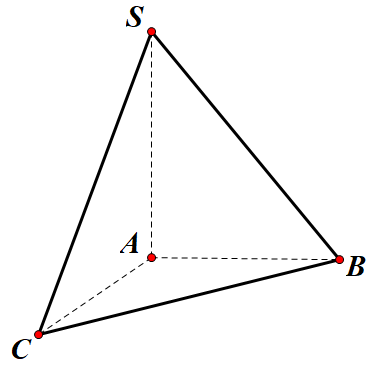
Do SA⊥(ABC)⇔(^SB,(ABC))=^SBA
Tam giác ABC vuông cân tại điểm A nên ta có 2.AB2=BC2⇔AB=a√2.
Trong tam giác vuông SAB, ta có tan^SBA=SAAB=a√62a√2=√3⇒^SBA=60∘
Xem thêm các bài tiếp theo bên dưới
- Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 0; 0) và đường thẳn
- Số đường tiệm cận của đồ thị hàm số y=2019x−3 là
- Cho số phức z thỏa mãn ˉz−5+2i=0. Modun của z bằng
- Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng $\Large a \
- Cho 9 điểm, trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu