Cho mạch điện xoay chiều gồm một điện trở thuần , cuộn cảm thuần và mộ

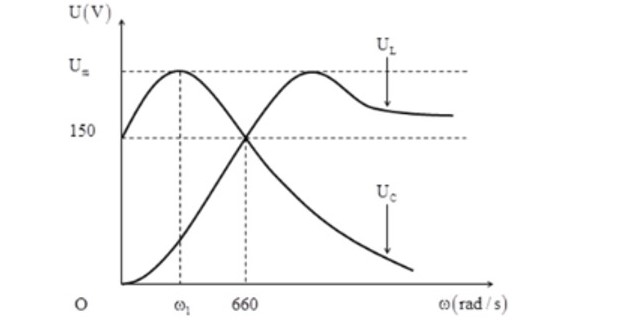
Cho mạch điện xoay chiều gồm một điện trở thuần , cuộn cảm thuần và một tụ điện mắc nối tiếp . Đặt vào hai đầu mạch điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số góc $\omega $ thay đổi được . Điện áp hiệu dụng giữa hai bản tụ điện và điện áp hiệu dụng hai đầu cuộn cảm lần lượt là $U_{C},U_{L}$  phụ thuộc vào $\omega $ , chúng được biểu diễn bằng các đồ thị như hình vẽ bên , tương ứng với các đường $U_{C},U_{L}$   . Khi $\omega ={{\omega }_{1}}$ thì là $U_{C}$ đạt cực đại $U_{m}$ Các giá trị $U_{m}$  và  ${{\omega }_{1}}$ lần lượt là :

• A.

  A. $150\sqrt{2}V,330\sqrt{3}rad/s$

• B.

  B. $100\sqrt{3}V,330\sqrt{3}rad/s$

• C.

  C.  $100\sqrt{3}V,330\sqrt{2}rad/s$

• D.

  D. $150\sqrt{2}V,330\sqrt{2}rad/s$

Hướng dẫn giải 
Ta có điện áp hiệu dụng ở hai đầu tụ điện được xác định bằng biểu thức:
${{U}_{C}}=\frac{U}{\sqrt{{{L}^{2}}{{C}^{2}}{{\omega }^{4}}-\left( 2LC-{{R}^{2}}{{C}^{2}} \right){{\omega }^{2}}+1}}$
${{\omega }_{C}}=\frac{2LC-{{R}^{2}}{{C}^{2}}}{2{{L}^{2}}{{C}^{2}}}$.
Hai giá trị của $\omega $ cho cùng ${{U}_{C}}$ thỏa mãn $\omega _{1}^{2}+\omega _{2}^{2}=2{{\omega }_{C}}$. Từ đồ thị ta thấy hai giá trị này là ${{\omega }_{1C}}=0rad/s$ và ${{\omega }_{2C}}=600rad/s\Rightarrow {{\omega }_{1}}=300\sqrt{3}rad/s$
Mặt khác điểm giao nhau của hai đồ thị này chính là ${{\omega }_{R}}$
${{U}_{C\max }}=\frac{U}{\sqrt{1-\left( \frac{{{\omega }_{C}}}{{{\omega }_{R}}} \right)}}=100\sqrt{3}V$