Đặt điện áp $u={{U}_{0}}\cos \left( 100\pi t \right)V$, t tính bằng s

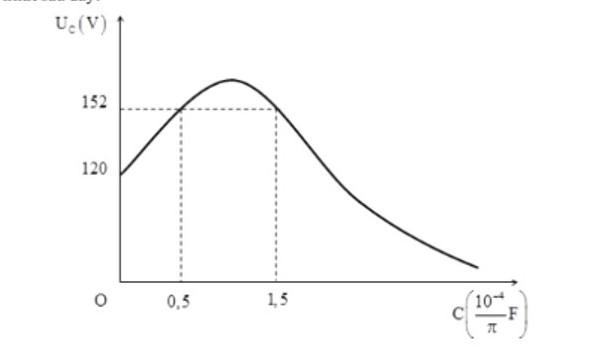
Đặt điện áp $u={{U}_{0}}\cos \left( 100\pi t \right)V$, t tính bằng s vào hai đầu đoạn mạch RLC mắc nối tiếp với cuộn dây thuần cảm. Trong đó $U_{0}$ ,R,L không đổi và C thay đổi được. Cho đồ thị thể hiện sự phụ thuộc của $U_{C}$ vào C như hình vẽ. Giá trị của R là gần giá trị nào nhất sau đây? 

• A.

  A. $120\Omega $

• B.

  B. $50\Omega $

• C.

  C. $60\Omega $

• D.

  D. $21\Omega $

Hướng dẫn giải
Điện áp hiệu dụng trên tụ điện
${{U}_{C}}=\frac{U{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\Rightarrow \left( {{R}^{2}}+Z_{L}^{2} \right)\frac{1}{Z_{C}^{2}}-2{{Z}_{L}}+1-{{\left( \frac{U}{{{U}_{C}}} \right)}^{2}}=0$
Hai giá trị của $Z_{C}$ cho cùng điện áp hiệu dụng trên $U_{C}$ thỏa mãn
$\frac{1}{{{Z}_{{{C}_{1}}}}}-\frac{1}{{{Z}_{C2}}}=\frac{1-{{\left( \frac{U}{{{U}_{C}}} \right)}^{2}}}{{{R}^{2}}+Z_{L}^{2}}$
$\frac{1}{{{Z}_{{{C}_{1}}}}}-\frac{1}{{{Z}_{C2}}}=\frac{2{{Z}_{L}}}{{{R}^{2}}+Z_{L}^{2}}$
$\Rightarrow R=21\Omega $