Cho mạch điện như hình vẽ, $\Large u=120\sqrt{2}cos(100\pi t) (V);$ cu

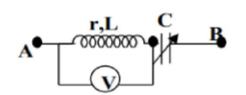
Cho mạch điện như hình vẽ, $\Large u=120\sqrt{2}cos(100\pi t) (V);$ cuộn dây $\Large r=15 \Omega, L=\dfrac{2}{25\pi} (H),$ C là tụ điện biến đổi. Điện trở vôn kế lớn vô cùng. Điều chỉnh C để số chỉ vôn kế lớn nhất. Tìm số chỉ vôn kế lúc này:

• A.

  $\Large C=\dfrac{10^{-2}}{8\pi} (F); U_V=136V.$

• B.

  $\Large C=\dfrac{10^{-2}}{3\pi} (F); U_V=136V.$

• C.

  $\Large C=\dfrac{10^{-2}}{5\pi} (F); U_V=186V.$

• D.

  $\Large C=\dfrac{10^{-2}}{4\pi} (F); U_V=163V.$

Phương pháp: 
Sử dụng lí thuyết về mạch điện xoay chiều có C thay đổi. 
Cảm kháng: $\Large Z_L=\omega L$
Số chỉ của vôn kế $\Large U_V=U_{rL}=\dfrac{U\sqrt{r^2+Z_L^2}}{\sqrt{r^2+(Z_L-Z_C)^2}}$
Cách giải:
Ta có: $\Large \left\{\begin{align} & r=15\Omega \\ & Z_L=\omega L=100\pi.\dfrac{2}{25\pi}=8\Omega \end{align}\right.$
Số chỉ của vôn kế: $\Large U_V=U_{rL}=\dfrac{U\sqrt{r^2+Z_L^2}}{\sqrt{r^2+(Z_L-Z_C)^2}}$
C thay đổi để $\Large U_{V max}$ khi mạch xảy ra cộng hưởng điện: $\Large Z_L=Z_C \Rightarrow C=\dfrac{1}{\omega^2L}=\dfrac{1}{(100\pi)^2.\dfrac{2}{25\pi}}=\dfrac{10^{-2}}{8\pi}F$
Số chỉ vôn kế lớn nhất: $\Large U_V=U_{rL}=\dfrac{U\sqrt{r^2+Z_L^2}}{\sqrt{r^2+(Z_L-Z_C)^2}}=\dfrac{120\sqrt{15^2+8^2}}{15}=136V$
Chọn A