Cho $\large \alpha, \,\, \beta$ là các số thực. Đồ thị hàm số $\large

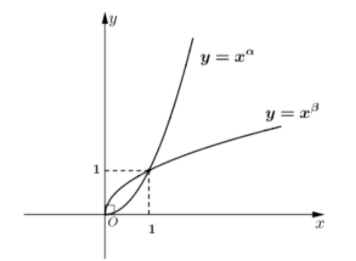
Cho $\large \alpha, \,\, \beta$ là các số thực. Đồ thị hàm số $\large y=x^{\alpha}, \,\, y=x^{\beta}$ trên khoảng $\large (0; +\infty)$ được cho trong hình vẽ  bên. Khẳng định nào sau đây đúng?

• A. A. $\large \alpha <0<1<\beta$
• B. B. $\large 0<\beta<1<\alpha$
• C. C. $\large 0<\alpha<1<\beta$
• D. D. $\large \beta<0<1<\alpha$

Chọn B

Ta thấy hàm số $\large y=x^{\alpha}, \,\, y=x^{\beta}$ đồng biến trên khoảng $\large (0; +\infty)$ nên $\large \alpha, \,\beta>0\Rightarrow $ Loại A, D

Lại có: với mỗi số $\large x_0>1$, ta có: $\large x_0^{\alpha}>x_0^{\beta}\Rightarrow \alpha >\beta \Rightarrow 0<\beta<1<\alpha$