Cho lăng trụ $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam giác vuông
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho lăng trụ $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam giác vuông tại $\large B, AB=1,AC=2$. Cạnh bên $\large AA'=\sqrt{2}$ .Hình chiếu vuông góc của $\large A'$ trên mặt $\large (ABC)$ trùng với chân đường cao hạ từ $\large B$ của tam giác $\large ABC$. Thể tích của khối lăng trụ đã cho bằng
Đáp án án đúng là: B
Lời giải chi tiết:
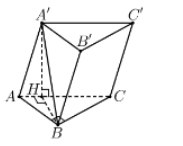
Tam giác vuông $\large ABC$, có $\large BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{3}$ và $\large AH=\frac{AB^{2}}{AC}=\frac{1}{2}$
Chiều cao khối lăng trụ $\large A'H=\sqrt{AA'^{2}-AH^{2}}=\frac{\sqrt{7}}{2}$
Diện tích tam giác $\large S_{\bigtriangleup ABC}=\frac{1}{2}AB.BC=\frac{\sqrt{3}}{2}$
Vậy thể tích khối lăng trụ $\large V_{ABC.A'B'C'}=S_{\bigtriangleup ABC}.A'H=\frac{\sqrt{21}}{4}$
Đáp án B
Xem thêm các bài tiếp theo bên dưới
- Cho lăng trụ $\large ABCD.A'B'C'D'$ có đáy $\large ABCD$ là hình chữ n
- Cho hình lăng trụ tam giác đều có cạnh đáy bằng $\large 2a$ và các mặt
- Cho hình chóp $\large S.ABCD$ có đáy là hình bình hành và có thể tích
- Cho hình hộp $\large ABCD.A'B'C'D'$. Gọi $\large M,N,P$ lần lượt là tr
- Cho khối lăng trụ tam giác $\large ABC.A'B'C'$. Gọi $\large M,N$ lần l