Cho hình chóp $\large S.ABCD$ có đáy là hình bình hành và có thể tích
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp $\large S.ABCD$ có đáy là hình bình hành và có thể tích bằng 48. Gọi $\large M,N$ lần lượt là các điểm thuộc các cạnh $\large AB,CD$ sao cho $\large MA=MB,NC=2ND$. Thể tích của khối chóp $\large S.MBCN$ bằng
Đáp án án đúng là: C
Lời giải chi tiết:
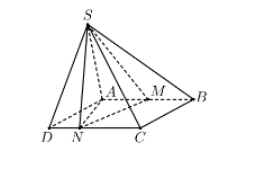
Gọi $\large d$ là khoảng cách từ đỉnh $\large A$ đến cạnh $\large CD$.
Diện tích hình bình hành: $\large S_{ABCD}=AB\cdot d$
Ta có: $\large S_{MBCN}=S_{ABCD}-S_{\bigtriangleup AMN}-S_{\bigtriangleup ADN}$
$\large =AB.d-\frac{1}{2}AM.d-\frac{1}{2}DN.d=AB.d-\frac{1}{4}AB.d-\frac{1}{6}AB.d=\frac{7}{12}AB.d=\frac{7}{12}S_{ABCD}$
Vậy $\large V_{S.MBCN}=\frac{7}{12}V_{S.ABCD}=\frac{7}{12}\cdot 48=28$
Đáp án C
Xem thêm các bài tiếp theo bên dưới
- Cho hình hộp $\large ABCD.A'B'C'D'$. Gọi $\large M,N,P$ lần lượt là tr
- Cho khối lăng trụ tam giác $\large ABC.A'B'C'$. Gọi $\large M,N$ lần l
- Cho hình chóp tứ giác đều $\large S.ABCD$. Mặt phẳng $\large (P)$ chứa
- Cho hình chóp $\large S.ABCD$ có đáy $\large ABCD$ là hình vuông cạnh
- Cho hình chóp tam giác đều $\large S.ABC$. Gọi $\large G$ là trọng tâm