Cho hình hộp $\large ABCD.A'B'C'D'$. Gọi $\large M,N,P$ lần lượt là tr

MỤC LỤC
Câu hỏi:
Cho hình hộp $\large ABCD.A'B'C'D'$. Gọi $\large M,N,P$ lần lượt là trung điểm của $\large AA',BC,CD$. Mặt phẳng $\large (MNP)$ chia khối hộp thành hai phần có thể tích là $\large V_{1},V_{2}$. Gọi $\large V_{1}$ là thể tích phần chứa điểm $\large C$, tỉ số $\large\frac{V_{1}}{V_{2}}$ bằng
Đáp án án đúng là: B
Lời giải chi tiết:
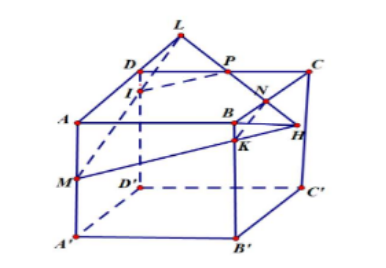
Gọi $\large NP\cap AB=H;NP\cap AD=L;ML\cap DD'=I;M H\cap B^{\prime}B=K$
Mặt phẳng $\large (MNP)$ cắt lập phương được ngũ giác $\large KNPIM$
Khi đó ta có $\large\bigtriangleup HBN=\bigtriangleup NCP=\bigtriangleup PDL(g.c.g) \Rightarrow HN=PL=\frac{HL}{3};\frac{HB}{HA}=\frac{HN}{HL}=\frac{1}{3};\frac{KB}{MA}=\frac{DI}{MA}=\frac{1}{3}$
Suy ra $\large V_{1}=V_{IBAMK}+V_{IABNPD}+V_{IKNB}=\frac{1}{3}S_{ADKM}.AD+\frac{1}{3}S_{ADNPQ}ID+\frac{1}{3}S_{DKN}DC$
$\large\frac{S_{ABKM}}{S_{ABB'A}}=\frac{BK+AM}{2AA'}=\frac{1}{3}\Rightarrow S_{ABKM}=\frac{1}{3}S_{ABB'A'}$
$\large S_{ABNPQ}=S_{ABCD}-S_{CNP}=\frac{7}{8}S_{ABCD}$
$\large S_{KBN}=\frac{1}{24}S_{BCC'B'}$
Đặc biệt hóa khối hộp chữ nhật là khối lập phương ta suy ra
$\large V_{1}=\frac{1}{3}\cdot \frac{1}{3}S_{ABB'A'}.AD+\frac{1}{3}\cdot \frac{DD'}{6}\cdot \frac{7}{8}S_{ABCD}+\frac{1}{3}DC\cdot \frac{1}{24}S_{BCC'B'}=\frac{25}{144}V$
Vậy $\large\frac{V_{1}}{V_{2}}=\frac{119}{25}$
Đáp án B
Xem thêm các bài tiếp theo bên dưới
- Cho khối lăng trụ tam giác $\large ABC.A'B'C'$. Gọi $\large M,N$ lần l
- Cho hình chóp tứ giác đều $\large S.ABCD$. Mặt phẳng $\large (P)$ chứa
- Cho hình chóp $\large S.ABCD$ có đáy $\large ABCD$ là hình vuông cạnh
- Cho hình chóp tam giác đều $\large S.ABC$. Gọi $\large G$ là trọng tâm
- Cho hình chóp $\large S.ABCD$ có đáy là hình chữ nhật, $\large AD=4$.