Cho khối hộp chữ nhật $\large ABCD.A'B'C'D'$ có $\large AA'=a\sqrt{3}$

MỤC LỤC
Câu hỏi:
Cho khối hộp chữ nhật $\large ABCD.A'B'C'D'$ có $\large AA'=a\sqrt{3}$. Biết rằng mặt phẳng $\large (A'BC)$ hợp với mặt đáy $\large (ABCD)$ một góc $\large 60^{\circ}$, đường thẳng $\large A'C$ hợp với mặt đáy $\large (ABCD)$ một góc $\large 30^{\circ}$. Thể tích của khối hộp chữ nhật đã cho bằng.
Đáp án án đúng là: C
Lời giải chi tiết:
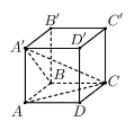
Xác định $\large\left\{\begin{align}30^{\circ}=\widehat{\left ( A'C;(ABCD) \right )}=\widehat{(A'C;AC)}=\widehat{A'CA}\\ 60^{\circ}=\widehat{\left ( (A'BC);(ABCD) \right )}=\widehat{(A' B;AB)}=\widehat{A'BA}\end{align}\right.$
Ta có $\large\left\{\begin{align}AB=AA'.\cot \widehat{A'BA}=a\\ AC=AA'.\cot \widehat{A'CA}=3a\end{align}\right.$ $\large\Rightarrow BC=\sqrt{AC^{2}-AB^{2}}=2a\sqrt{2}$
Vậy thể tích khối hộp chữ nhật $\large V_{ABCD.A'B'C'D'}=AA'.AB.BC=2a^{3}\sqrt{6}$
Đáp án C
Xem thêm các bài tiếp theo bên dưới
- Cho hình hộp chữ nhật có đường chéo $\large d=\sqrt{21}$. Độ dài ba kí
- Cho lăng trụ $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam giác vuông
- Cho lăng trụ $\large ABCD.A'B'C'D'$ có đáy $\large ABCD$ là hình chữ n
- Cho hình lăng trụ tam giác đều có cạnh đáy bằng $\large 2a$ và các mặt
- Cho hình chóp $\large S.ABCD$ có đáy là hình bình hành và có thể tích