Cho khối chóp tứ giác $\large S.ABCD$ có thể tích $\large V$, đáy là h

Cho khối chóp tứ giác $\large S.ABCD$ có thể tích $\large V$, đáy là hình bình hành. Gọi $\large M,N,P,Q$ lần lượt là trung điểm các cạnh $\large SB,BC,CD,DA$. Thể tích khối chóp $\large M.CNQP$ bằng

• A.

  A. $\large\frac{3V}{4}$

• B.

  B. $\large\frac{3V}{8}$

• C.

  C. $\large\frac{V}{16}$

• D.

  D. $\large\frac{3V}{16}$

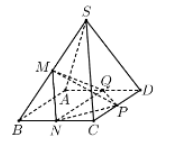
Từ giả thiết suy ra $\large S_{CNQP}=S_{CNQD}-S_{DPQ}=\frac{1}{2}S_{ABCD}-\frac{1}{8}S_{ABCD}=\frac{3}{8}S_{ABCD}$

Vì $\large M$ là trung điểm $\large SB$ nên

$\large d(M;(ABCD))=\frac{1}{2}d(S;(ABCD))$

Suy ra $\large V_{M.CNQP}=V_{M.CNQP}=\frac{1}{3}.d\left ( M, (ABCD) \right ).S_{CNQP}=\frac{1}{3}.\frac{1}{2}.d\left ( A, (ABCD) \right ).\frac{3}{8}S_{ABCD}=\frac{3}{16}V$

Đáp án D