Trong các khối chóp tứ giác đều $\large S.ABCD$ mà khoảng cách từ $\la

Trong các khối chóp tứ giác đều $\large S.ABCD$ mà khoảng cách từ $\large A$ đến mặt phẳng $\large (SBC)$ bằng $\large 2a$, khối chóp có thể tích nhỏ nhất bằng 

• A.

  A. $\large 3\sqrt{3}a^{3}$

• B.

  B. $\large 4\sqrt{3}a^{3}$

• C.

  C. $\large 2\sqrt{3}a^{3}$

• D.

  D. $\large 2a^{3}$

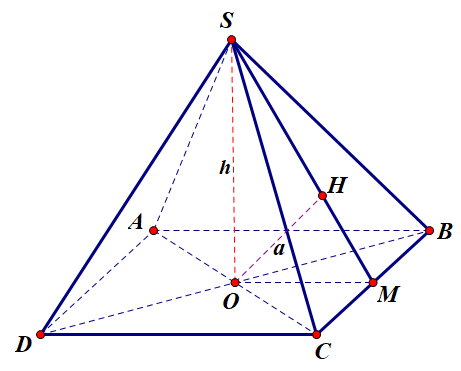
Gọi $\large O$ là tâm của mặt đáy, $\large M$ là trung điểm cạnh $\large BC$

Dễ thấy do $\large S.ABCD$ là khối chóp tứ giác đều nên $\large ABCD$ là hình vuông và $\large SO\perp (ABCD)$

Gọi $\large H$ là chân đường vuông góc hạ từ $\large O$ xuống $\large SM$ trong mặt phẳng $\large (SMO)\Rightarrow OH\perp SM$ (1)

Hơn nữa, $\large OM\perp BC$ và $\large SM\perp BC\Rightarrow BC\perp (SOM)\Rightarrow OH\perp BC$ (2)

Từ (1) và (2) $\large\Rightarrow OH\perp (SBC)\Rightarrow d(O;(SBC))=OH$

Do $\large O$ là trung điểm cạnh $\large AC$ nên $\large d(A;(SBC))=2d(O;(SBC))=2OH$

Theo giả thiết $\large d(A;(SBC))=2a\Rightarrow OH=a$

Giả sử chiều dài cạnh đáy là $\large 2x(x>a$ do $\large OM>OH)$ và $\large SO=h(h>0)$

Trong tam giác vuông $\large SOM$

$\large OH^{2}=\frac{SO^{2}.OM^{2}}{SO^{2}+OM^{2}}=\frac{h^{2}x^{2}}{h^{2}+x^{2}}\Rightarrow a^{2}=\frac{h^{2}x^{2}}{h^{2}+x^{2}}\Rightarrow h^{2}(x^{2}-a^{2})=a^{2}x^{2}\Rightarrow h^{2}=\frac{a^{2}x^{2}}{x^{2}-a^{2}}$

Thể tích khối chóp là $\large S.ABCD$ là

$\large V=\frac{1}{3}h\cdot (4x^{2})\Leftrightarrow V^{2}=\frac{16}{9}h^{2}x^{4}\Leftrightarrow V^{2}=\frac{16}{9}\cdot \frac{a^{2}x^{2}}{x^{2}-a^{2}}x^{4}\Leftrightarrow V^{2}=\frac{16a^{2}}{9}\cdot \frac{x^{6}}{x^{2}-a^{2}}$

Xét hàm số $\large f(x)=\frac{16a^{2}}{9}\cdot \frac{x^{6}}{x^{2}-a^{2}}$ trên khoảng $\large(a;+\infty )$ ta có

$\large {f}'(x)=\frac{16{{a}^{2}}}{9}.\frac{4{{x}^{7}}-6{{x}^{5}}{{a}^{2}}}{{{\left( {{x}^{2}}-{{a}^{2}} \right)}^{2}}}=\frac{16a^{2}}{9}\cdot \frac{4x^{7}-6x^{5}a^{2}}{(x^{2}-a^{2})^{2}}$

$\large {f}'(x)=0$ $\large\Leftrightarrow \left\{\begin{align}x=0\\ x=\pm \sqrt{\frac{3}{2}}a\end{align}\right.$

Ta có BBT:

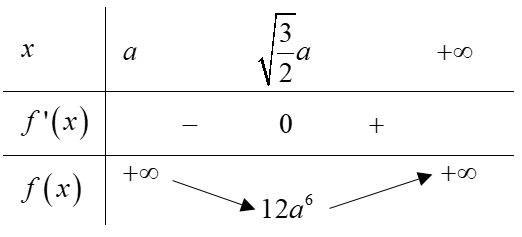
Hàm số $\large f(x)$ đạt giá trị nhỏ nhất là $\large 12a^{6}$ nên khối chóp có thể tích nhỏ nhất bằng $\large  2\sqrt{3}a^{3}$

Đáp án C