Cho khối chóp $\large S.ABCD$ có thể tích bằng 1, đáy $\large ABCD$ là

Cho khối chóp $\large S.ABCD$ có thể tích bằng 1, đáy $\large ABCD$ là hình thang với cạnh đáy lớn là $\large AD$ và $\large AD=3BC$. Gọi $\large M$ là trung điểm cạnh $\large SA,N$ là điểm thuộc cạnh $\large CD$ sao cho $\large ND=3NC$. Mặt phẳng $\large (BMN)$ cắt cạnh $\large SD$ tại $\large P$. Thể tích khối chóp $\large A.MBNP$ bằng:

• A.

  A. $\large\frac{3}{8}$

• B.

  B. $\large\frac{5}{12}$

• C.

  C. $\large\frac{5}{16}$

• D.

  D. $\large\frac{9}{32}$

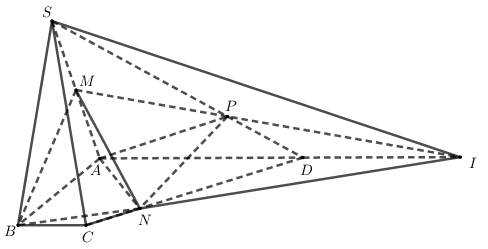
Đặt $\large V=V_{S.ABCD}=1$

Gọi $\large I$ là giao điểm của $\large BN$ với $\large AD$, suy ra $\large P$ là giao điểm của $\large MI$ với $\large SD$.

$\large BC//DI$ và $\large ND=3NC\Rightarrow DI=3BC\Rightarrow D$ là trung điểm của $\large AI$

Do đó $\large P$ là trọng ttâm của tam giác $\large SAI\Rightarrow \frac{SP}{SD}=\frac{2}{3}$

$\large S_{BCN}=\frac{1}{4}S_{BCD}=\frac{1}{4}\cdot \frac{1}{4}S_{ABCD}=\frac{1}{16}S_{ABCD};S_{ADN}=S_{NID}=9S_{BCN}=\frac{9}{16}S_{ABCD}$

$\large S_{ABN}=S_{ABCD}-S_{BCN}-S_{ADN}=\frac{3}{8}S_{ABCD}$ 

Suy ra $\large V_{S.ABN}=\frac{3}{8}V;V_{S.ADN}=\frac{9}{16}V$

$\large V_{S.MBN}=\frac{1}{2}V_{S.ABN}\Rightarrow V_{A.BMN}=\frac{1}{2}V_{S.ABN}=\frac{3}{16}V$

$\large V_{S.MNP}=\frac{1}{2}V_{S.ANP}\Rightarrow V_{A.MNP}=\frac{1}{2}V_{S.ANP}=\frac{1}{2}\cdot \frac{2}{3}V_{S.AND}=\frac{3}{16}V$

Do đó $\large V_{A.MBNP}=V_{A.BMN}+V_{A.MNP}=\frac{3}{8}V=\frac{3}{8}$

Đáp án A