Cho khối chóp S. ABC có đáy là tam giác vuông tại A , AC= 2AB = 2a . H

Cho khối chóp S. ABC có đáy là tam giác vuông tại A , AC= 2AB = 2a . Hình chiếu của S trên mặt phẳng (ABC) là trung điểm của đoạn thẳng BC và góc giữa các mặt phẳng (SAB) và (ABC) bằng $\large 60^\circ$. Gọi M , N lần lượt là các điểm sao cho $\large \overline{BM}=2.\overline{AS}$ và $\large \overline{CN}=3.\overline{AS}$. Tính thể tích của khối đa diện ABCSMN theo a .

• A. A. $\large \dfrac{4\sqrt{3}}{3}a^3$
• B. B. $\large 2\sqrt{3}a^3$
• C. C. $\large 3\sqrt{3}a^3$
• D. D. $\large \dfrac{2\sqrt{3}}{3}a^3$

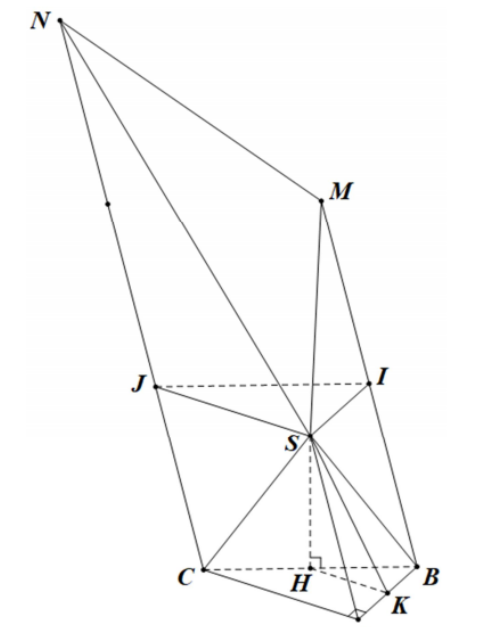
Gọi H là hình chiếu của S lên (ABC), K là trung điểm của AB

Ta có: $\large \left(\widehat{(SAB), (ABC)} \right )=\left(\widehat{(SM), (HK)} \right )=\widehat{SKH}=60^\circ$

Xét tam giác AHK vuông tại H, ta có: $\large SH=HK.\tan 60^\circ=\dfrac{1}{2}AC.\tan 60^\circ=a\sqrt{3}$

Thể tích khối chọp S.ABC là $\large V_{S.ABC}=\dfrac{1}{3}.\dfrac{1}{2}.AB.AC.SH=\dfrac{a^3\sqrt{3}}{3}$

Ta có: $\large V_{ABCSMN}=V_{ABCSIJ}+V_{SIJNM}$

+ Xét hình lăng trụ ABCSIJ, ta có: $\large V_{ABCSIJ}=3V_{S.ABC}=a^3\sqrt{3}$

+ Xét hình chóp SIJNM có: 

$\large V_{SIJNM}=\dfrac{1}{3}.d(S, (IJNM)).S_{IJNM}=\dfrac{1}{3}.d(S, (IJCB)).\dfrac{3}{2}.S_{BCIJ}$ 

$\large =\dfrac{3}{2}.V_{SBCJI}=\dfrac{3}{2}.\dfrac{2}{3}.V_{ABCSIJ}=a^3\sqrt{3}$

Do đó: $\large $