Cho khối chóp S.ABCD có đáy ABCD là hình thoi, góc $\large \widehat{AB

Cho khối chóp S.ABCD có đáy ABCD là hình thoi, góc $\large \widehat{ABC}=60^\circ$, $\large SA=SB=2a$. Biết rằng góc giữa các mặt phẳng $\large (SAB), \,\, (SCD)$ và mặt phẳng $\large (ABCD)$ bằng nhau, góc giữa mặt phẳng $\large (SAD)$ và mặt đáy bằng $\large \alpha$ với $\large \tan\alpha =\dfrac{2\sqrt{19}}{3}$. Tính thể tích khối chóp S.ABCD

• A. A. $\large \dfrac{\sqrt{19}}{4}a^3$
• B. B. $\large \dfrac{\sqrt{57}}{16}a^3$
• C. C. $\large \dfrac{\sqrt{57}}{8}a^3$
• D. D. $\large \dfrac{\sqrt{19}}{8}a^3$

Chọn D

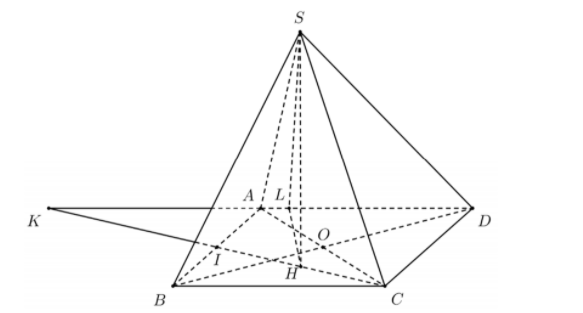
Dễ thấy $\large \Delta ABC$ và $\large \Delta ADC$ là các tam giác đều. Đặt x là độ dài cạnh của hình thoi ABCD

Gọi H là hình chiếu của S lên mp (ABCD), I là trung điểm của AB

Vì SA = SB nên $\large \Delta SAH=\Delta SBH\Rightarrow HA=HB$ hay H thuộc đường trung trực CI của AB

Dễ thấy: $\large (\widehat{(SAB), (ABCD)})=\widehat{SIH}$ và $\large (\widehat{(SCD), (ABCD)})=\widehat{SCH}$

Vì $\large \widehat{SIH}=\widehat{SCH}\Rightarrow \Delta SIH=\Delta SCH\Rightarrow IH=HC$ hay H là trung điểm của IC

Gọi K là giao điểm của CI và AB, L là hình chiếu của H lên AD

Dễ thấy: $\large HK=\dfrac{3}{4}CK$ do đó $\large HL=\dfrac{3}{4} d(C, AD)=\dfrac{3\sqrt{3}}{8}.x$

$\large \alpha=(\widehat{(SAD), (ABCD)})=\widehat(SLH)\Rightarrow SH=HL.\tan\alpha=\dfrac{3\sqrt{3}}{8}x.\dfrac{2\sqrt{19}}{3}=\dfrac{\sqrt{57}}{4x}$ 

$\large AH=\sqrt{AI^2+IH^2}=\sqrt{\left(\dfrac{x}{2} \right )^2+\left(\dfrac{\sqrt{3}}{4}x \right )^2}=\dfrac{\sqrt{7}}{4}x$

$\large SA^2=AH^2+SH^2\Leftrightarrow (2a)^2=\dfrac{7}{16}x^2+\dfrac{57}{16}x^2=4x^2\Rightarrow x=1$ 

Suy ra: $\large SH=\dfrac{\sqrt{57}}{4}a$ và $\large S_{ABCD}=2S_{ABC}=2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{2}$

Thể tích $\large S.ABCD$ là: $\large V_{S.ABCD}=\dfrac{1}{3}S_{ABCD}.SH=\dfrac{1}{3}.\dfrac{a^2\sqrt{3}}{2}.\dfrac{\sqrt{57}}{4}a=\dfrac{\sqrt{19}}{8}a^3$