Có tất cả bao nhiêu giá trị nguyên của tham số thực m để phương trình

Có tất cả bao nhiêu giá trị nguyên của tham số thực m để phương trình $\large \left| x^3-3x^2\right| -mx=4$ có đúng 4 nghiệm thực phân biệt?

• A. A. 1
• B. B. 0
• C. C. 3
• D. D. 2

Chọn A

Nhận xét: $\large x=0$ không phải là nghiệm của phương trình $\large \left|x^3-3x^2\right| -mx=4$, do đó: 

$\large \left|x^3-3x^2\right|-mx=4\Leftrightarrow m=\dfrac{\left|x^3-3x^2\right|-4}{x}$

Đặt $\large f(x)=\dfrac{\left|x^3-3x^2\right|-4}{x}=\dfrac{\left|x^2(x-3)-4\right|}{x}$

Ta có: $\large f(x)=$ $\large \left\{\begin{align}& \dfrac{x^3-3x^2-4}{x}\,\, \text{khi }\, x\geq 3\\& \dfrac{-x^3+3x^2-4}{x}\,\, \text{khi }\, x<3, \forall x\neq 0\\\end{align}\right.$ $\large \Rightarrow f'(x)=$ $\large \left\{\begin{align}& \dfrac{2x^3-3x^2+4}{x^2}\,\, \tetx{khi }\, x\geq 3\\& \dfrac{-2x^3+3x^2+4}{x^2}\,\,\text{khi }\, x<3, \forall x\neq 0\\\end{align}\right.$

+) $\large \dfrac{2x^3-3x^2+4}{x^2}=\dfrac{x^2(2x-3)+4}{x^2}>0, \forall x\geq 3$

+) $\large \dfrac{02x^3+3x^2+4}{x^2}=0\Leftrightarrow x=2$

Lập bảng biến thiên của hàm số $\large y=f(x)$

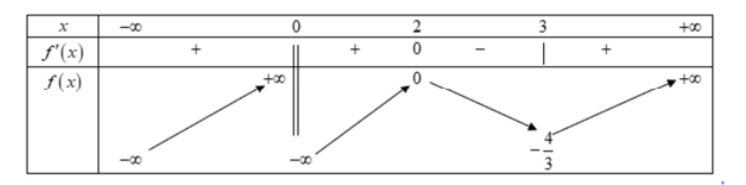
Dựa vào bảng biến thiên ta thấy đường thẳng $\large y=m$ cắt đồ thị hàm số $\large y=f(x)$ tại 4 điểm phân biệt khi $\large -\dfrac{4}{3}

Kết luận: Có một giá trị nguyên của m để phương trình đã cho có đúng 4 nghiệm thực phân biệt.