Cho khối chóp $\large S.ABCD$ có $\large SA \perp ( ABCD), SA = 2a\sqr

Cho khối chóp $\large S.ABCD$ có $\large SA \perp ( ABCD), SA = 2a\sqrt {3}$, tứ giác ABCD là hình chữ nhật có $\large AB = a$, $\large AD = a \sqrt {3}$. Góc giữa đường thẳng SC và mặt phẳng $\large ABCD$ bằng

$\large 60^{\circ}$

• A.

  $\large 60^{\circ}$

• B.

  $\large 90^{\circ}$

• C.

  $\large 30^{\circ}$

• D.

  $\large 45^{\circ}$

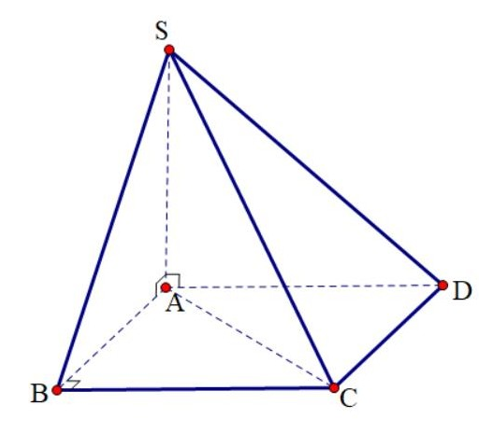
Ta có $\large SA \perp (ABCD)$ nên suy ra hình chiếu của SC trên mặt phẳng $\large ABCD$ là AC
$\large \Rightarrow (SC, ( ABCD)) = (SC, AC) = \widehat{SCA}$
$\large AC = \sqrt {AB^{2} + BC^{2}} = 2a$
$\large tan \widehat{SCA} = \dfrac {SA}{AC} = \sqrt {3} \Rightarrow \widehat{SCA} = 60^{\circ}$