Cho hình nón có góc ở đỉnh bằng $\Large 60^{\circ}$, diện tích xung qu

Cho hình nón có góc ở đỉnh bằng $\Large 60^{\circ}$, diện tích xung quanh bằng $\Large 6\pi a^2$. Tính thể tích của khối nón đã cho.

• A.

  $\Large V=\dfrac{3\pi a^3\sqrt{2}}{4}.$

• B.

  $\Large V=\dfrac{\pi a^3\sqrt{2}}{4}.$

• C.

  $\Large V=3\pi a^3.$

• D.

  $\Large V=\pi a^3.$

Chọn C

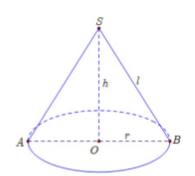
Hình nón có góc ở đỉnh bằng $\Large 60^{\circ}$ nên thiết diện qua trục SAB là tam giác đều, do đó $\Large l=SB=2OB=2r$.

Mà $\Large S_{xq}=\pi rl=\pi 2r^2=6\pi a^2 \Rightarrow r=a\sqrt{3}$. Đường cao $\Large h=SO=\dfrac{(2r)\sqrt{3}}{2}=r\sqrt{3}=3a$

Vậy thể tích khối nón $\Large V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi .(a\sqrt{3})^2.3a=3a^3\pi$.