Cho hình lập phương ABCD.A'B'C'D' cạnh a . Gọi M, N, P lần lượt là tâm

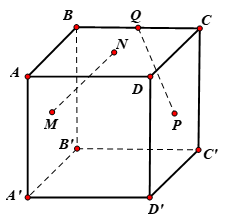
Cho hình lập phương ABCD.A'B'C'D' cạnh a . Gọi M, N, P lần lượt là tâm của các hình vuông ABB'A', ABCD, CDD'C' và Q là trung điểm của BC (minh họa như hình vẽ). Khoảng cách giữa hai đường thẳng MN và PQ bằng

• A. $\large a\sqrt{2}$
• B. $\large \dfrac{a\sqrt{6}}{6}$
• C. $\large \dfrac{a\sqrt{3}}{6}$
• D. $\large \dfrac{a\sqrt{6}}{4}$

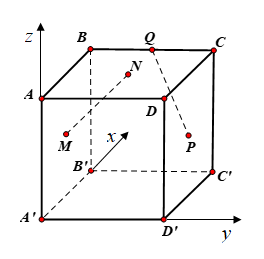
Gắn hệ toạ độ Oxyz trong đó $\large A'\equiv O,\,\, A(0; 0; a), \,\, D'(0; a; 0), \,\, B'(a; 0; 0)$

Khi đó: $\large B(a, 0, a),\,\, D(0; a; a),\,\, C'(a; a; 0), \,\, C(a; a; a;)$

Do M, N, P lần lượt là tâm của các hình vuông $\large ABB'A', ABCD, CDD'C'$ và Q là trung điểm của BC nên $\large M\left(\dfrac{a}{2}; 0; \dfrac{a}{2} \right ), N\left(\dfrac{a}{2}; \dfrac{a}{2}; a \right ), Q\left(a; \dfrac{a}{2}; a\right ), P\left(\dfrac{a}{2}; a; \dfrac{a}{2} \right )$

Ta có: $\large \overrightarrow{MN}=\left(0;\dfrac{a}{2}; \dfrac{a}{2}  \right ), \overrightarrow{QP}=\left(-\dfrac{a}{2}; \dfrac{a}{2}; -\dfrac{a}{2} \right ), \overrightarrow{MQ}=\left(\dfrac{a}{2}; \dfrac{a}{2}; \dfrac{a}{2} \right )$

Gọi $\large \overrightarrow{u_1}; \overrightarrow{u_2}$ lần lượt là vecto chỉ phương MN, PQ

Khoảng cách giữa hai đường thẳng MN và PQ bằng: 

$\large d(MN, PQ)=\dfrac{\left|\left[\overrightarrow{u_1},\overrightarrow{u_2} \right ].\overrightarrow{MQ}\right|}{\left|\overrightarrow{u_1},\overrightarrow{u_2}\right|}=\dfrac{|a|}{\sqrt{6}}=\dfrac{a\sqrt{6}}{6}$