Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 1. G

Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 1. Gọi E, F lần lượt là trung điểm các cạnh AA' và BB'; đường thẳng CE cắt đường thẳng C'A' tại E', đường thẳng CF cắt đường thẳng C'B' tại F'. Thể tích của khối đa diện A'EE'B'FF' bằng

• A. A. $\Large \dfrac{\sqrt{3}}{12}$
• B. B. $\Large \dfrac{\sqrt{3}}{2}$
• C. C. $\Large \dfrac{\sqrt{3}}{3}$
• D. D. $\Large \dfrac{\sqrt{3}}{6}$

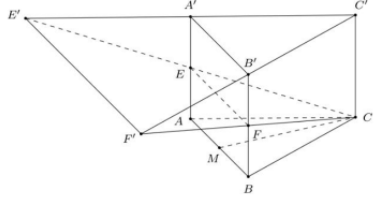
Thể tích khối lăng trụ tam giác đều ABC.A'B'C' là

$\Large V_{ABC.A'B'C'} = S_{ABC}.AA' = \dfrac{\sqrt{3}}{4}.1 = \dfrac{\sqrt{3}}{4}$

Gọi M là trung điểm AB. Suy ra $\Large CM \perp (ABB'A')$ và $\Large CM = \dfrac{\sqrt{3}}{2}$

Thể tích khối chóp C.ABFE là

$\Large V_{C.ABFE} = \dfrac{1}{3}.S_{ABFE}.CM = \dfrac{1}{3}.1.\dfrac{1}{2}.\dfrac{\sqrt{3}}{2} = \dfrac{\sqrt{3}}{12}$

Thể tích khối đa diện A'B'C'EFC là

$\Large V_{A'B'C'EFC} = V_{ABC.A'B'C'} - V_{C.ABFE} = \dfrac{\sqrt{3}}{4} - \dfrac{\sqrt{3}}{12} = \dfrac{\sqrt{3}}{6}$

Ta dễ dàng chứng minh được A' và B' lần lượt là trung điểm C'E' và C'F'

Thể tích khối chóp C.C'E'F' là

$\Large V_{C.C'E'F'} = \dfrac{1}{3}.S_{C'E'F'}.CC' = \dfrac{1}{3}.4.S_{C'A'B'}.CC' = \dfrac{1}{3}.4.\dfrac{\sqrt{3}}{4}.1 = \dfrac{\sqrt{3}}{3}$

Khi đó, thể tích khối đa diện EFA'B'E'F' là

$\Large V_{EFA'B'E'F'} = V_{C.C'E'F'} - V_{A'B'C'EFC} = \dfrac{\sqrt{3}}{3} - \dfrac{\sqrt{3}}{6} = \dfrac{\sqrt{3}}{6}$