Cho hình chóp đều $\Large S.ABC$ có chiều cao bằng $\Large a$, cạnh bê

Cho hình chóp đều $\Large S.ABC$ có chiều cao bằng $\Large a$, cạnh bên bằng $\Large 2a.$ Tính thể tích $\Large V$ của khối chóp $\Large S.ABC.$

• A.

  A. $\Large V=\dfrac{a^3\sqrt{3}}{12}.$

• B.

  B. $\Large \dfrac{9a^3\sqrt{3}}{4}.$

• C.

  C. $\Large \dfrac{3a^3\sqrt{3}}{4}.$

• D.

  D. $\Large V=\dfrac{a^3\sqrt{3}}{4}.$

Chọn C

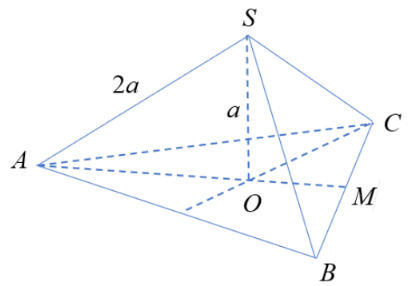
Gọi $\Large O$ là tâm tam giác đều $\Large ABC$, $\Large M$ là trung điểm của $\Large BC.$

Khi đó $\Large SO$ là đường cao của hình chóp đều $\Large S.ABC.$

Ta có: $\Large AM=\dfrac{3}{2}AO$ $\Large =\dfrac{3}{2}\sqrt{SA^2-SO^2}$ $\Large =\dfrac{3a\sqrt{3}}{2}.$

$\Large BC=2BM$ $\Large =2.AM\tan{\widehat{BAM}}$ $\Large =2.\dfrac{3a\sqrt{3}}{2}.\tan{30^{\circ}}$ $\Large =3a.$
Thể tích $\Large V$ của khối chóp $\Large S.ABC$ là:

$\Large V=\dfrac{1}{3}.SO.S_{\Delta ABC}$ $\Large =\dfrac{1}{3}.SO.\dfrac{1}{2}.AM.BC$ $\Large =\dfrac{1}{3}.a.\dfrac{1}{2}.\dfrac{3a\sqrt{3}}{2}.3a$ $\Large =\dfrac{3a^3\sqrt{3}}{4}.$